题目内容
9.袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是$\frac{1}{3}$,从B中摸出一个红球的概率为p.(1)从A中又放回的摸球,每次摸出一个,共摸5次
①恰好有3次摸到红球的概率;②第一次、第三次、第五次摸到红球的概率.
(2)若A、B两个袋子中的球之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是$\frac{2}{5}$,求p的值.
分析 (1)①利用相互独立事件的概率公式运算求得结果.
②由于每次摸出一个红球的概率都是$\frac{1}{3}$,即可求出第一次、第三次、第五次摸到红球的概率.
(2)设袋子A中有m个球,袋子B中有2m个球,由$\frac{{\frac{1}{3}m+2mp}}{3m}=\frac{2}{5}$,求得p的值.
解答 解:(1)①由于每次摸出一个红球的概率是$\frac{1}{3}$,摸不到红球的概率为$\frac{2}{3}$,故恰好有3次摸到红球的概率$C_5^3×{({\frac{1}{3}})^3}×{({\frac{2}{3}})^2}=\frac{40}{243}$.
②由于每次摸出一个红球的概率都是$\frac{1}{3}$,故第一次、第三次、第五次摸到红球的概率为${({\frac{1}{3}})^3}=\frac{1}{27}$.
(Ⅱ)设袋子A中有m个球,袋子B中有2m个球,
由$\frac{{\frac{1}{3}m+2mp}}{3m}=\frac{2}{5}$,得$p=\frac{13}{30}$
点评 本题主要考查相互独立事件的概率乘法公式、及n次独立重复试验中恰好发生k次的概率公式的应用,属于中档题.

练习册系列答案
相关题目
17.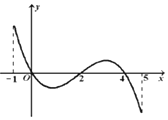 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,
f(x)的导函数y=f′(x)的图象(该图象关于(2,0)中心对称) 如图所示.
下列关于f(x)的命题:
①函数f(x)的极大值点为 0与4;
②函数f(x)在[0,2]上是减函数;
③函数y=f(x)-a零点的个数可能为0、1、2、3、4个;
④如果当时x∈[-1,t],f(x)的最大值是2,那么t的最大值为5;.
⑤函数f(x)的图象在[2,4]是上凸的
其中一定正确命题的序号是①②④.
 已知函数f(x)的定义域为[-1,5],部分对应值如表,
已知函数f(x)的定义域为[-1,5],部分对应值如表,| x | -1 | 0 | 4 |
| f(x) | 1 | 2 | 2 |
下列关于f(x)的命题:
①函数f(x)的极大值点为 0与4;
②函数f(x)在[0,2]上是减函数;
③函数y=f(x)-a零点的个数可能为0、1、2、3、4个;
④如果当时x∈[-1,t],f(x)的最大值是2,那么t的最大值为5;.
⑤函数f(x)的图象在[2,4]是上凸的
其中一定正确命题的序号是①②④.
4.一个几何体的三视图如图所示,该几何体的体积为( )


| A. | 24-π | B. | 24-3π | C. | $8-\frac{4π}{3}$ | D. | $8-\frac{8π}{3}$ |
1.在△ABC中,$a=2,b=4,C={30°},则\overrightarrow{BC}•\overrightarrow{CA}$=( )
| A. | $4\sqrt{3}$ | B. | 4 | C. | -4$\sqrt{3}$ | D. | -4 |
19.已知数列{an}为等差数列,满足$\overrightarrow{OA}={a_3}\overrightarrow{OB}+{a_{2016}}\overrightarrow{OC}$,其中A,B,C在一条直线上,O为直线AB外一点,记数列{an}的前n项和为Sn,则S2018的值为( )
| A. | $\frac{2017}{2}$ | B. | 2017 | C. | $\frac{2018}{2}$ | D. | 2018 |
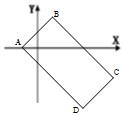 如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.
如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.