题目内容
求实半轴长a为3,离心率e为
,焦点在x轴上双曲线的标准方程.
| 5 |
| 3 |
考点:双曲线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:设出双曲线的方程,求得a=3,由离心率公式可得c=5,再由a,b,c的关系,求得b,即可得到双曲线的方程.
解答:
解:设双曲线的方程为
-
=1(a>0,b>0)
由于a=3,e=
=
,
则c=5,
即有b=
=
=4,
则双曲线的方程为
-
=1.
| x2 |
| a2 |
| y2 |
| b2 |
由于a=3,e=
| c |
| a |
| 5 |
| 3 |
则c=5,
即有b=
| c2-a2 |
| 25-9 |
则双曲线的方程为
| x2 |
| 9 |
| y2 |
| 16 |
点评:本题考查双曲线的方程和性质,考查离心率公式的运用,考查运算能力,属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
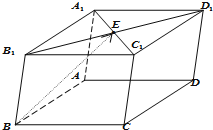
如图所示,在平行六面体ABCD-A1B1C1D1中,点E为上底面对角线A1C1的中点,若
=
+x
+y
,则( )
| BE |
| AA1 |
| AB |
| AD |

A、x=-
| ||||
B、x=
| ||||
C、x=-
| ||||
D、x=
|
 如图,平面直角坐标系中,动点P(x,y),PM⊥y轴,垂足为M,点N与点P关于x轴对称,且
如图,平面直角坐标系中,动点P(x,y),PM⊥y轴,垂足为M,点N与点P关于x轴对称,且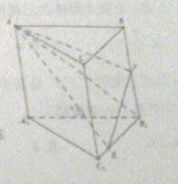 如图,已知三棱柱ABC-A1B1C1中BB1⊥平面ABC,且AC⊥BC1,AA1=3,AC=CB=2.E,F分别为线段B1C1,BB1上的动点.
如图,已知三棱柱ABC-A1B1C1中BB1⊥平面ABC,且AC⊥BC1,AA1=3,AC=CB=2.E,F分别为线段B1C1,BB1上的动点.