题目内容

已知正项数列{an}满足an2-（n2+n-1）an-n2-n=0，求数列{an}的通项公式．
考点：数列递推式
专题：计算题,等差数列与等比数列
分析：由已知条件推导出[an-（n2+n）]（an+1）=0，由此能求出数列{an}的通项公式．
解答： 解：∵an2-（n2+n-1）an-（n2+n）=0，
∴[an-（n2+n）]（an+1）=0．
∵{an}是正项数列，
∴an=n2+n．
点评：本题考查数列的通项公式的求法，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
如表给出一个“三角形数阵”：
1
4
   
1
2
1
4
  
3
4
3
8
3
16
 
…   
已知每一列的数成等差数列，从第三行起，每一行的数成等比数列，每一行的公比都相等，记第i行第j列的数为aij（i≥j，i，j∈N*），
（1）求a83；
（2）试写出aij关于i，j的表达式；
（3）记第n行的和为An，求数列{An}的前m项和Bm的表达式．
某市为控制大气PM2.5的浓度，环境部门规定：该市每年的大气主要污染物排放总量不能超过55万吨，否则将采取紧急限排措施．已知该市2013年的大气主要污染物排放总量为40万吨，通过技术改造和倡导绿色低碳生活等措施，此后每年的原大气主要污染物排放量比上一年的排放总量减少10%．同时，因经济发展和人口增加等因素，每年又新增加大气主要污染物排放量胁（m＞0）万吨．
（Ⅰ）从2014年起，该市每年大气主要污染物排放总量（万吨）依次构成数列{an}，求相邻两年主要污染物排放总量的关系式；
（Ⅱ）证明：数列{an-10m}是等比数列；
（Ⅲ）若该市始终不需要采取紧急限排措施，求m的取值范围．
设函数f（x）=x+
a
x
+b（a＞b＞0），求f（x）的单调区间，并证明f（x）在其单调区间上的单调性．
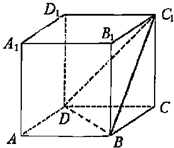已知ABCD-A1B1C1D1是棱长为1的正方体．
（1）求异面直线BC1与B1D1所成的角．
（2）求直线BC1与平面ABCD所成的角．
（3）求二面角C1-BD-A的正切值．
对于函数y=sin4x+cos4x周期为
 
．
已知f（x）=
x，0＜x≤1
2f(x-1)，x＞1
，则f（
3
2
）=
 
．
某地区对两所高中学校进行学生体质状况抽测，甲校有学生800人，乙校有学生500人，现用分层抽样的方法在这1300名学生中抽取一个样本．已知在甲校抽取了48人，则在乙校应抽取学生人数为
 
．
函数y=2sin（
1
2
x+
π
3
）单调增区间为：
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网