题目内容
把函数y=sin(
-x)cos(x+
)的图象向右平移a(a>0)个单位,得到的函数y=g(x)的图象关于直线x=
对称.
(Ⅰ)求a的最小值;
(Ⅱ)就a的最小值求函数y=g(x)在区间[-
,
]上的值域.
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
(Ⅰ)求a的最小值;
(Ⅱ)就a的最小值求函数y=g(x)在区间[-
| π |
| 12 |
| π |
| 3 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)利用诱导公式对函数解析式化简整理,根据g(x)的图象关于直线x=
对称,求得a的值的集合,最后根据a的范围求得a的最小值.
(2)先求得函数解析式,根据x的范围确定2x的范围,最后根据正弦函数的性质求得其最大和最小值.
| π |
| 4 |
(2)先求得函数解析式,根据x的范围确定2x的范围,最后根据正弦函数的性质求得其最大和最小值.
解答:
解:(1)y=sin(
-x)cos(x+
)=sin(x+
)cos(x+
)=
sin(2x+
)=
cos2x,
∴g(x)=
cos(2x-2a),它关于直线x=
对称,
∴2×
-2a=kπ,k∈Z,
∴a=-
+
,
∵a>0,
∴a的最小值为
,
(2)由(1)知g(x)=
cos(2x-
)=
sin2x,
∵-
≤x≤
,
∴-
≤2x≤
,
∴-
≤sin2x≤1,
∴-
≤g(x)≤
即g(x)的值域为[-
,
]
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
∴g(x)=
| 1 |
| 2 |
| π |
| 4 |
∴2×
| π |
| 4 |
∴a=-
| kπ |
| 2 |
| π |
| 4 |
∵a>0,
∴a的最小值为
| π |
| 4 |
(2)由(1)知g(x)=
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
∵-
| π |
| 12 |
| π |
| 3 |
∴-
| π |
| 6 |
| 2π |
| 3 |
∴-
| 1 |
| 2 |
∴-
| 1 |
| 4 |
| 1 |
| 2 |
即g(x)的值域为[-
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题主要考查了三角函数图象与性质,三角函数恒等变换的应用.解题时注意结合三角函数的图象.

练习册系列答案
相关题目
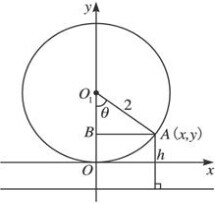 如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面0.5米.风车圆周上一点A从最低点O开始,运动t秒后与地面的距离为h米.以O为原点,过点O的圆的切线为x轴,建立直角坐标系.
如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面0.5米.风车圆周上一点A从最低点O开始,运动t秒后与地面的距离为h米.以O为原点,过点O的圆的切线为x轴,建立直角坐标系.