题目内容
已知函数f(x)=x2+ax+b(a、b∈R),且集合A={x|x=f(x)},B={x|x=f[f(x)]}.
(1)求证:A⊆B;
(2)当A={-1,3}时,用列举法表示B.
(1)求证:A⊆B;
(2)当A={-1,3}时,用列举法表示B.
考点:集合的包含关系判断及应用,集合的表示法
专题:综合题,集合
分析:(1)若x∈A,则x=f(x)成立,则f[f(x)]=f(x)=x必成立,进而根据集合包含关系的定义,得到结论;
(2)由A={x|f(x)=x}={x|x2+ax+b=x}={x|x2+(a-1)x+b=0}={-1,3},结合方程根与系数关系可求a,b,进而可求,f(x),然后代入B={x|f[f(x)]=x}整理可求.
(2)由A={x|f(x)=x}={x|x2+ax+b=x}={x|x2+(a-1)x+b=0}={-1,3},结合方程根与系数关系可求a,b,进而可求,f(x),然后代入B={x|f[f(x)]=x}整理可求.
解答:
(1)证明:若x∈A,则x=f(x)成立,
则f[f(x)]=f(x)=x必成立,即x∈B,
故A⊆B;
(2)解:∵A={x|f(x)=x}={x|x2+ax+b=x}={x|x2+(a-1)x+b=0}={-1,3}
∴-1,3是方程x2+(a-1)x+b=0的根
∴
,即a=-1,b=-3,
∴f(x)=x2-x-3
∴B={x|f[f(x)]=x}={x|f(x2-x-3)=x}={x|(x2-x-3)2-(x2-x-3)-3=x}
化简可得,(x2-x-3)2-x2=0
∴(x2-3)(x2-2x-3)=0
∴x=
或x=-
或x=3或x=-1
∴B={
,-
,-1,3}.
则f[f(x)]=f(x)=x必成立,即x∈B,
故A⊆B;
(2)解:∵A={x|f(x)=x}={x|x2+ax+b=x}={x|x2+(a-1)x+b=0}={-1,3}
∴-1,3是方程x2+(a-1)x+b=0的根
∴
|
∴f(x)=x2-x-3
∴B={x|f[f(x)]=x}={x|f(x2-x-3)=x}={x|(x2-x-3)2-(x2-x-3)-3=x}
化简可得,(x2-x-3)2-x2=0
∴(x2-3)(x2-2x-3)=0
∴x=
| 3 |
| 3 |
∴B={
| 3 |
| 3 |
点评:本题主要考查了二次函数与二次方程之间关系的相互转化,方程的根与系数关系的应用.

练习册系列答案
相关题目
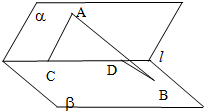 如图,已知二面角α-l-β为60°,点A∈α,AC⊥l,C为垂足,点B∈β,BD⊥l,D为垂足,且AC=2,CD=3,DB=1,则AB的长度为( )
如图,已知二面角α-l-β为60°,点A∈α,AC⊥l,C为垂足,点B∈β,BD⊥l,D为垂足,且AC=2,CD=3,DB=1,则AB的长度为( )