题目内容
14.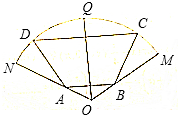 如图,扇形MON的半径为2,圆心角为$\frac{2}{3}$π,四边形ABCD为扇形的内接等腰梯形,其中底边AB的两个端点分别在半径ON和0M上,C、D在弧$\widehat{MQN}$上,Q为弧$\widehat{MN}$的中点,∠ABC=$\frac{2}{3}$π,求梯形ABCD面积的最大值.
如图,扇形MON的半径为2,圆心角为$\frac{2}{3}$π,四边形ABCD为扇形的内接等腰梯形,其中底边AB的两个端点分别在半径ON和0M上,C、D在弧$\widehat{MQN}$上,Q为弧$\widehat{MN}$的中点,∠ABC=$\frac{2}{3}$π,求梯形ABCD面积的最大值.
分析 设OB=2x,(0<x<2),根据三角函数的关系式,分别求出梯形的上底,下底和高,利用换元法,结合三角函数的辅助角公式转化为三角函数,利用三角函数的最值问题进行求解即可.
解答 解:设OB=2x,(0<x<2),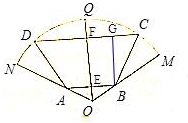
则OE=x,BE=$\sqrt{3}$x,
在△OBC中,OB=2x,OC=2,∠OBC=$\frac{5π}{6}$
cos$\frac{5π}{6}$=$\frac{O{B}^{2}+B{C}^{2}-O{C}^{2}}{2OB•BC}$,得BC=$\sqrt{4-{x}^{2}}$-$\sqrt{3}x$,
∵∠CBG=$\frac{π}{6}$,∴CG=$\frac{1}{2}$($\sqrt{4-{x}^{2}}$-$\sqrt{3}x$),
BG=$\frac{\sqrt{3}}{2}$($\sqrt{4-{x}^{2}}$-$\sqrt{3}x$),FC=BE+CG=$\frac{\sqrt{4-{x}^{2}}+\sqrt{3}x}{2}$,
S=$\frac{\sqrt{3}}{4}(\sqrt{4-{x}^{2}}+3\sqrt{3}x)(\sqrt{4-{x}^{2}}-\sqrt{3}x)$=$\frac{\sqrt{3}}{4}(4-10{x}^{2}+2\sqrt{3}x•\sqrt{4-{x}^{2}})$,
令x=2sinα,0<α<$\frac{π}{2}$,
则S=$\frac{\sqrt{3}}{4}$(4-40sin2α+4$\sqrt{3}$sinα•2cosα)
=$\frac{\sqrt{3}}{4}$(4$\sqrt{3}$sin2α+4-40×$\frac{1-cos2α}{2}$)
=$\frac{\sqrt{3}}{4}$(4$\sqrt{3}$sin2α+20cos2α-16)
=$\sqrt{3}$($\sqrt{3}$sin2α+5cos2α-4)
=$\sqrt{3}$[2$\sqrt{7}$($\frac{\sqrt{3}}{2\sqrt{7}}$sin2α+$\frac{5}{2\sqrt{7}}$cos2α-4]
令cosβ$\frac{\sqrt{3}}{2\sqrt{7}}$,sinβ=$\frac{5}{2\sqrt{7}}$,
则S=$\sqrt{3}$[2$\sqrt{7}$sin(2α+β)-4],
∴当sin(2α+β)=1时,S取得最大值,
此时S=$\sqrt{3}$(2$\sqrt{7}$-4)=2$\sqrt{21}$-4$\sqrt{3}$.
点评 本题主要考查三角函数的应用问题,根据条件求出梯形的上底,下底,高结合梯形的面积公式,利用辅助角公式进行化简是解决本题的关键.综合性较强,难度较大.

| A. | 8π | B. | 5π | C. | $\frac{4\sqrt{3}}{3}$π | D. | 4$\sqrt{3}$π |
| A. | p∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | (¬p)∨q |
| A. | 1 | B. | 26 | C. | 35 | D. | 36 |
| A. | 递增数列 | B. | 递减数列 | C. | 常数列 | D. | 摆动数列 |