题目内容
抛物线y2=
x上的一点M到焦点的距离为1，则点M到y轴的距离是（ ）
| 1 |
| 4 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据抛物线点到焦点的距离等于点到准线的距离，可得所求点的横坐标，即可求得结论．
解答：
解：抛物线y2=
x的准线方程为x=-
．
∵抛物线y2=
x上的一点M到焦点的距离为1，
∴根据抛物线点到焦点的距离等于点到准线的距离，可得所求点的横坐标为
，
∴点M到y轴的距离为
．
故选D．
| 1 |
| 4 |
| 1 |
| 16 |
∵抛物线y2=
| 1 |
| 4 |
∴根据抛物线点到焦点的距离等于点到准线的距离，可得所求点的横坐标为
| 15 |
| 16 |
∴点M到y轴的距离为
| 15 |
| 16 |
故选D．
点评：本题考查抛物线的定义，考查学生的计算能力，属于基础题．
练习册系列答案
金钥匙试卷系列答案
相关题目
已知集合P={x，y，z}，Q={1，2，3}，映射f：P→Q中满足f（y）=2的映射的个数共有（ ）
| A、2 | B、4 | C、6 | D、9 |
以O为中心，F1，F2为两个焦点的椭圆上存在一点M，满足|
|=2|
|=2|
|，则该椭圆的离心率为（ ）
| MF1 |
| MO |
| MF2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知全集U={1，2，3，4，5}，A={2，4，5}，则∁uA=（ ）
| A、∅ |
| B、{1，2，4} |
| C、{2，4，5} |
| D、{1，3} |
在区间[-2π，2π]范围内，函数y=tanx与函数y=sinx的图象交点的个数为（ ）
| A、3 | B、5 | C、7 | D、9 |
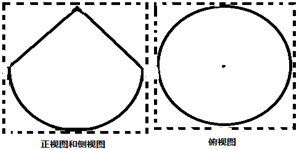如图实线所示，一个几何体的正视图和侧视图相同，俯视图为圆形，该几何体的三视图恰好可放在边长为2的正方形内（图中虚线所示），则该几何体的体积为（ ）A、1+
| ||
| B、2+π | ||
| C、π | ||
D、
|
y=sinx+
cosx（0≤x≤
），则y的最小值为（ ）
| 3 |
| π |
| 2 |
| A、-2 | ||
| B、-1 | ||
| C、1 | ||
D、
|
已知P（
，
）在角α的终边上，则sinα的值是（ ）
| 1 |
| 2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
甲船在A处发现乙船在北偏东60°的B处，乙船正以a n mile/h的速度向北行驶．已知甲船的速度是