题目内容
8．
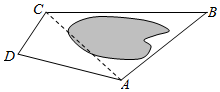如图，为了测量A，C两点间的距离，选取同一平面上B、D两点，测出四边形ABCD各边的长度（单位：km）：AB=5，BC=8，CD=3，DA=5，且∠B与∠D互补，则AC的长为7km．
分析 分别在△ABC和△ACD中使用余弦定理解出AC，列方程解出cosD，得出AC．
解答 7 解：在△ABC中，由余弦定理得AC2=AB2+BC2-2AB×BCcosB=89-80cosB，
在△ACD中，由余弦定理得AC2=CD2+AD2-2AD×CDcosD=34-30cosD，
∴89-80cosB=34-30cosD，
∵A+C=180°，∴cosB=-cosD，
∴cosD=-$\frac{1}{2}$，
∴AC2=34-30×（-$\frac{1}{2}$）=49．
∴AC=7．
故答案为7．
点评 本题考查了余弦定理的应用，属于中档题．
练习册系列答案
相关题目
18．已知函数f（x）=2x2-4的图象上一点（1，-2）及邻近一点（1+△x，-2+△y），则$\frac{△y}{△x}$等于（ ）
| A． | 4 | B． | 4△x | C． | 4+2△x | D． | 4+2（△x）2 |
16．在△ABC中，a=4，b=$\frac{5}{2}$，5cos（B+C）+3=0，则角B的大小为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{6}$或$\frac{5π}{6}$ |
3．若椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与双曲线$\frac{3{x}^{2}}{{a}^{2}}$-$\frac{3{y}^{2}}{{b}^{2}}$=1共焦点，则双曲线的渐近线方程为（ ）
| A． | y=±$\frac{\sqrt{2}}{2}$x | B． | y=±$\sqrt{2}$x | C． | y=±$\frac{1}{2}$x | D． | y=±2x |
某商店根据以往某种玩具的销售纪录，绘制了日销售量的频率分布直方图，如图所示．，将日销售量落入各组的频率视为概率，并假设每天的销售量互相独立．