题目内容
18.已知a,b,c分别为△ABC内角A,B,C的对边,A=$\frac{π}{4}$,a=2,bcosC-ccosB=2$\sqrt{2}$,则∠B=$\frac{5π}{8}$.分析 根据正弦定理将边化角,利用三角函数的恒等变换化简得出B,C的关系,结合三角形的内角和解出B.
解答 解:∵bcosC-ccosB=2$\sqrt{2}$,∴sinBcosC-sinCcosB=$\sqrt{2}$sinA.
即sin(B-C)=1.∴B-C=$\frac{π}{2}$.
∵B+C=π-A=$\frac{3π}{4}$,
∴B=$\frac{5π}{8}$.
故答案为:$\frac{5π}{8}$.
点评 本题考查了正弦定理在解三角形中的应用,属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
6.已知等差数列{an}的前n项和为Sn,若a1=1,a2=-1,则S4=( )
| A. | 6 | B. | -6 | C. | 8 | D. | -8 |
13.某班5位同学分别选择参加数学、物理、化学这3个学科的兴趣小组,每人限选一门学科,则每个兴趣小组都至少有1人参加的不同选择方法种数为( )
| A. | 150 | B. | 180 | C. | 240 | D. | 540 |
7.下列命题中正确的是( )
| A. | cosα≠0是α≠2kπ+$\frac{π}{2}$(k∈Z)的充分必要条件 | |
| B. | 函数f(x)=3ln|x|的零点是(1,0)和(-1,0) | |
| C. | 设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=$\frac{1}{2}$-p | |
| D. | 若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差会改变 |
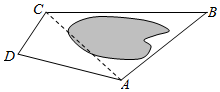 如图,为了测量A,C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为7km.
如图,为了测量A,C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为7km.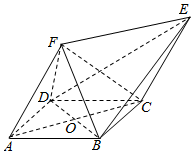 如图所示的几何体中,ABCD为菱形,ACEF为平行四边形,△BDF为等边三角形,O为AC与BD的交点.
如图所示的几何体中,ABCD为菱形,ACEF为平行四边形,△BDF为等边三角形,O为AC与BD的交点.