题目内容
设点A(x1,y1)、B(x2,y2)是函数y=f(x)(x1<x<x2)图象上的两端点.O为坐标原点,且点N满足
=λ
+(1-λ)
,点M(x,y)在函数y=f(x)的图象上,且满足x=λx1+(1-λ)x2(λ为实数),则称|MN|的最大值为函数y=f(x)的“高度”.函数f(x)=x2-2x-1在区间[-1,3]上的“高度”为 .
| ON |
| OA |
| OB |
考点:平面向量的基本定理及其意义
专题:函数的性质及应用,平面向量及应用
分析:根据函数f(x)高度的定义,想法求出点M,N的坐标即可表示出|MN|,求其最大值即可:A(-1,2),B(3,2),x1=-1,x2=3,所以便可求出N(3-4λ,2),M(3-4λ,16λ2-16λ+2),所以得到|MN|=16|λ2-λ|,而根据M点在f(x)图象上可求出0≤λ≤1,这样根据二次函数的图象即可求得|λ2-λ|的最大值,从而求出f(x)在区间[-1,3]上的“高度”.
解答:
解:根据已知条件,A(-1,2),B(3,2);
∴λ
+(1-λ)
=λ(-1,2)+(1-λ)(3,2)=(3-4λ,2);
∴N(3-4λ,2);
xM=-λ+3(1-λ)=3-4λ;
M点在f(x)图象上;
∴M点的纵坐标为:16λ2-16λ+2,且-1≤3-4λ≤3,即0≤λ≤1;
∴M(3-4λ,16λ2-16λ+2);
∴|MN|=16|λ2-λ|;
∴λ=
时|λ2-λ|取到最大值
,从而|MN|取最大值4;
∴f(x)在[-1,3]上的高度为4.
故答案为:4.
∴λ
| OA |
| OB |
∴N(3-4λ,2);
xM=-λ+3(1-λ)=3-4λ;
M点在f(x)图象上;
∴M点的纵坐标为:16λ2-16λ+2,且-1≤3-4λ≤3,即0≤λ≤1;
∴M(3-4λ,16λ2-16λ+2);
∴|MN|=16|λ2-λ|;
∴λ=
| 1 |
| 2 |
| 1 |
| 4 |
∴f(x)在[-1,3]上的高度为4.
故答案为:4.
点评:考查对函数“高度”定义的理解,向量的坐标和点的坐标的关系,以及根据二次函数的图象求最值,并且弄清函数|λ2-λ|和二次函数λ2-λ图象的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
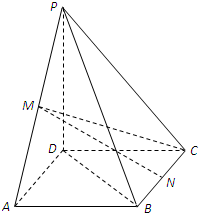 如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别是PA,PB的中点,PD⊥平面ABCD,且PD=AD=
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别是PA,PB的中点,PD⊥平面ABCD,且PD=AD=
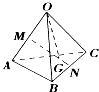 如图所示,已知空间四边形OABC,其对角线为OB,AC,M,N分别为OA,BC的中点,点G在线段MN上,且
如图所示,已知空间四边形OABC,其对角线为OB,AC,M,N分别为OA,BC的中点,点G在线段MN上,且