题目内容
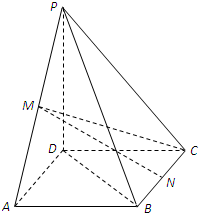 如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别是PA,PB的中点,PD⊥平面ABCD,且PD=AD=
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别是PA,PB的中点,PD⊥平面ABCD,且PD=AD=| 2 |
(Ⅰ)证明:MN∥平面PCD;
(Ⅱ)证明:MC⊥BD.
考点:直线与平面平行的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)证明:取AD中点E,连结ME,NE,由已知M,N分别是PA,BC的中点,得到ME∥PD,NE∥CD,利用面面平行的判定定理得到所证;
(Ⅱ)因为PD⊥平面ABCD,利用线面垂直的性质定理得PD⊥DA,PD⊥DC,建立空间直角坐标系,分别写出D,A,B,C,P的坐标,判断向量
,
的位置关系.
(Ⅱ)因为PD⊥平面ABCD,利用线面垂直的性质定理得PD⊥DA,PD⊥DC,建立空间直角坐标系,分别写出D,A,B,C,P的坐标,判断向量
| MC |
| BD |
解答:
 (Ⅰ)证明:取AD中点E,连结ME,NE,…(2分)
(Ⅰ)证明:取AD中点E,连结ME,NE,…(2分)
由已知M,N分别是PA,BC的中点,
所以ME∥PD,NE∥CD,…(4分)
所以,平面MNE∥平面PCD,…(7分)
所以,MN∥平面PCD.…(8分)
(Ⅱ)证明:因为PD⊥平面ABCD,所以PD⊥DA,PD⊥DC,
在矩形ABCD中,AD⊥DC,
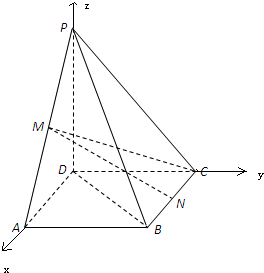
如图,建立空间直角坐标系,…(9分)
则D(0,0,0),A(
,0,0),B(
,1,0),C(0,1,0),P(0,0,
).…(10分)
所以M(
,0,
),
=(-
,-1,0),
=(-
,1,-
),…(11分)
因为
•
=0,所以MC⊥BD.…(13分)
 (Ⅰ)证明:取AD中点E,连结ME,NE,…(2分)
(Ⅰ)证明:取AD中点E,连结ME,NE,…(2分)由已知M,N分别是PA,BC的中点,
所以ME∥PD,NE∥CD,…(4分)
所以,平面MNE∥平面PCD,…(7分)
所以,MN∥平面PCD.…(8分)
(Ⅱ)证明:因为PD⊥平面ABCD,所以PD⊥DA,PD⊥DC,
在矩形ABCD中,AD⊥DC,
如图,建立空间直角坐标系,…(9分)
则D(0,0,0),A(
| 2 |
| 2 |
| 2 |
所以M(
| ||
| 2 |
| ||
| 2 |
| BD |
| 2 |
| MC |
| ||
| 2 |
| ||
| 2 |
因为
| MC |
| BD |
点评:本题考查了面面平行的性质定理和判定定理以及利用空间向量证明线线垂直,体现了向量的工具性.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目

 则
则 的值为 ( )
的值为 ( ) C. 3 D. 0
C. 3 D. 0
 B.
B. 
 D.
D. 
 的棱长为
的棱长为 ,点
,点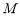 在棱
在棱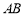 上,且
上,且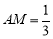 ,点
,点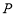 是平面
是平面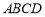 上的动点,且动点
上的动点,且动点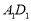 的距离与点
的距离与点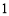 ,则动点
,则动点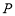 的轨迹是 ( )
的轨迹是 ( )