题目内容
5.已知$\overrightarrow a,\overrightarrow b$是两个非零向量,且$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|+|{\overrightarrow b}|$,则下列说法正确的是( )| A. | $\overrightarrow a+\overrightarrow b=\overrightarrow 0$ | B. | $\overrightarrow a=\overrightarrow b$ | ||
| C. | $\overrightarrow a$与$\overrightarrow b$共线反向 | D. | 存在正实数λ,使$\overrightarrow a=λ\overrightarrow b$ |
分析 由题意,两边同时平方,化简可得$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为0°,即可得到结论
解答 解:∵$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|+|{\overrightarrow b}|$,
∴(|$\overrightarrow{a}$+$\overrightarrow{b}$|)2=(|$\overrightarrow{a}$|+|$\overrightarrow{b}$|)2,
∴|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,
∴$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为0°,
∵$\overrightarrow a,\overrightarrow b$是两个非零向量
∴存在正实数λ,使$\overrightarrow a=λ\overrightarrow b$,
故选:D
点评 本题考查了向量的数量积公式和向量的模的运算以向量的共线定理,属于基础题

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
16.已知m,n是两条不重合的直线,α,β,γ是三个两两不重合的平面,给出下列四个命题:
①若m⊥α,m⊥β,则α∥β;
②若α⊥γ,β⊥γ,则α∥β;
③若m?α,n?β,m∥n,则α∥β;
④若m,n是异面直线,m?α,m∥β,n∥α,则α∥β.
其中真命题是( )
①若m⊥α,m⊥β,则α∥β;
②若α⊥γ,β⊥γ,则α∥β;
③若m?α,n?β,m∥n,则α∥β;
④若m,n是异面直线,m?α,m∥β,n∥α,则α∥β.
其中真命题是( )
| A. | ①和④ | B. | ①和③ | C. | ③和④ | D. | ①和② |
13.已知点A,B,C,D在边长为1的方格点图的位置如图所示,则向量$\overrightarrow{AD}$在$\overrightarrow{AB}$方向上的投影为( )

| A. | -$\frac{\sqrt{5}}{5}$ | B. | -1 | C. | -$\frac{2\sqrt{13}}{13}$ | D. | $\frac{\sqrt{5}}{5}$ |
17.连续抛掷两枚骰子,第一枚骰子和第二枚骰子点数之差是一个随机变量X,则“X>4”表示的实验结果是( )
| A. | 第一枚6点,第二枚2点 | B. | 第一枚5点,第二枚1点 | ||
| C. | 第一枚1点,第二枚6点 | D. | 第一枚6点,第二枚1点 |
14.数列{an}为正项等比数列,若a3=3,且an+1=2an+3an-1(n∈N,n≥2),则此数列的前5项和S5等于( )
| A. | $\frac{121}{3}$ | B. | 41 | C. | $\frac{119}{3}$ | D. | $\frac{241}{9}$ |
15.已知离散型随机变量X服从二项分布X~B(n,p)且E(X)=12,D(X)=3,则n与p的值分别为( )
| A. | $18,\frac{2}{3}$ | B. | $16,\frac{3}{4}$ | C. | $16,\frac{1}{4}$ | D. | $18,\frac{1}{4}$ |
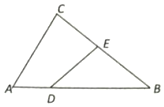 如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=3AD,BC=2BE.
如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=3AD,BC=2BE.