题目内容
5.若方程$\frac{{x}^{2}}{9-k}$-$\frac{{y}^{2}}{4-k}$=1表示焦点在x轴上的椭圆,则实数k的取值范围是4<k<$\frac{13}{2}$.分析 根据题意,将方程变形为$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{k-4}$=1,由焦点在x轴上的椭圆的标准方程的特点可得9-k>k-4>0,解可得k的值,即可得答案.
解答 解:根据题意,方程$\frac{{x}^{2}}{9-k}$-$\frac{{y}^{2}}{4-k}$=1可以变形为$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{k-4}$=1,
若其表示焦点在x轴上的椭圆,则有9-k>k-4>0,
解可得4<k<$\frac{13}{2}$;
故答案为:4<k<$\frac{13}{2}$.
点评 本题考查椭圆的标准方程,掌握焦点在x轴上的椭圆的标准方程的特点是解题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
15.某几何体的三视图如图所示,则该几何体的体积为( )
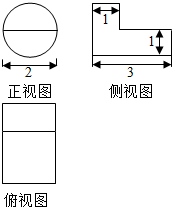

| A. | 6π+4 | B. | π+4 | C. | $\frac{5π}{2}$ | D. | 2π |
13.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )


| A. | 2 | B. | 4 | C. | 6 | D. | 12 |
20.椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$的左、右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为4,A、B两点的坐标分别为(x1,y1)和(x2,y2),则|y2-y1|的值为( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{20}{3}$ | D. | $\frac{5}{3}$ |
10.执行如图所示的程序框图,若输出的S=945,则判断框中应填入( )


| A. | i<6? | B. | i<7? | C. | i<9? | D. | i<10? |
14.下列说法正确的是( )
| A. | 抛一枚硬币10次,一定有5次正面向上 | |
| B. | 明天本地降水概率为70%,是指本地下雨的面积是70% | |
| C. | 互斥事件一定是对立事件,对立事件不一定是互斥事件 | |
| D. | 若A与B为互斥事件,则P(A)+P(B)≤1 |