题目内容
解关于x的不等式：（x-3）（x+4）≥0．
考点：一元二次不等式的解法
专题：计算题,不等式的解法及应用
分析：先求对应方程的根，然后借助函数的图象可得不等式的解集．
解答：
解：（x-3）（x+4）=0的两根为-4、3，
又y=（x-3）（x+4）的图象开口向上，
∴：（x-3）（x+4）≥0的解集为{x|x≤-4或x≥3}．
又y=（x-3）（x+4）的图象开口向上，
∴：（x-3）（x+4）≥0的解集为{x|x≤-4或x≥3}．
点评：该题考查一元二次不等式的解法，属基础题，深刻理解“三个二次”间的关系是解题关键．
练习册系列答案
相关题目
已知f′（x）为f（x）的导数，若f′（x）＜f（x）对于任意的x∈R都成立，则（ ）
A、f（0）＜
| ||
B、f（0）＞
| ||
C、f（0）=
| ||
D、
|
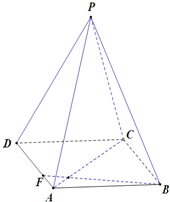如图所示，正四棱锥P=ABCD中，AB=1，侧棱PA与底面ABCD所成角的正切值为