题目内容
1.在△ABC中,cos2A-3cos(B+C)=1,△ABC的面积为$5\sqrt{3},b=5$,则sinBsinC=$\frac{5}{7}$.分析 利用倍角公式和诱导公式即可得出A;由三角形的面积公式c=4.由余弦定理得a.通过正弦定理求解即可.
解答 解:由cos2A-3cos(B+C)=1,得2cos2A+3cosA-2=0,
即(2cosA-1)(cosA+2)=0,解得cosA=$\frac{1}{2}$或cosA=-2(舍去).
因为0<A<π,所以A=$\frac{π}{3}$.
由S=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc=5$\sqrt{3}$,得到bc=20.又b=5,解得c=4.
由余弦定理得a2=b2+c2-2bccosA=25+16-20=21,故a=$\sqrt{21}$.
又由正弦定理得sinBsinC=$\frac{b}{a}$sinA•$\frac{c}{a}$sinA=$\frac{bc}{{a}^{2}}$sin2A=$\frac{20}{21}$×$\frac{3}{4}$=$\frac{5}{7}$.
故答案为:$\frac{5}{7}$.
点评 本题考查三角形的解法,熟练掌握三角函数的倍角公式和诱导公式、三角形的面积公式、余弦定理、正弦定理是解题的关键.

练习册系列答案
相关题目
17.已知在数列{an}中,a1=$\frac{4}{5}$,an+1=$\left\{\begin{array}{l}{2{a}_{n},{a}_{n}∈[0,\frac{1}{2}]}\\{2{a}_{n}-1,{a}_{n}∈(\frac{1}{2},1]}\end{array}\right.$,则a2015等于( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
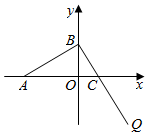 如图,已知A(-4a,0)(a>0),B、C两点分别在y轴和x轴上运动,并且满足$\overrightarrow{AB}$•$\overrightarrow{BQ}$=0,$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{CQ}$.
如图,已知A(-4a,0)(a>0),B、C两点分别在y轴和x轴上运动,并且满足$\overrightarrow{AB}$•$\overrightarrow{BQ}$=0,$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{CQ}$.