题目内容
15.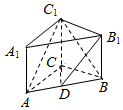 如图,已知侧棱垂直底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,点D是AB的中点.
如图,已知侧棱垂直底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,点D是AB的中点.(1)求证:AC⊥BC;
(2)求证:AC1∥平面CDB1.
分析 (1)利用勾股定理能证明AC⊥BC.
(2)以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,利用向量法能证明AC1∥平面CDB1.
解答 证明:(1)∵AC=3,AB=5,BC=4
∴AC2+BC2=AB2,
∴AC⊥BC.
(2)以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,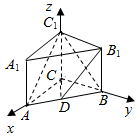
设CC1=t,则由题意得A(3,0,0),C1(0,0,t),C(0,0,0),
B(0,4,0),D($\frac{3}{2}$,2,0),B1(0,4,t),
$\overrightarrow{CD}$=($\frac{3}{2},2,0$),$\overrightarrow{C{B}_{1}}$=(0,4,t),$\overrightarrow{A{C}_{1}}$=(-3,0,t),
设平面CDB1的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CD}=\frac{3}{2}x+2y=0}\\{\overrightarrow{n}•\overrightarrow{C{B}_{1}}=4y+tz=0}\end{array}\right.$,取x=2,得$\overrightarrow{n}$=(4,-3,$\frac{12}{t}$),
∴$\overrightarrow{A{C}_{1}}•\overrightarrow{n}$=0,
∵AC1?平面CDB1,∴AC1∥平面CDB1.
点评 本题考查两直线垂直的证明,考查线面平行的证明,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
13.一个等差数列的前4项是a,x,b,2x,则$\frac{a}{b}$等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
3.已知向量$\overrightarrow a=(-4,3)$,$\overrightarrow b=(5,6)$,则3|$\overrightarrow a{|^2}$$-4\overrightarrow a•\overrightarrow b$=( )
| A. | 83 | B. | 63 | C. | 57 | D. | 23 |
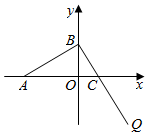 如图,已知A(-4a,0)(a>0),B、C两点分别在y轴和x轴上运动,并且满足$\overrightarrow{AB}$•$\overrightarrow{BQ}$=0,$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{CQ}$.
如图,已知A(-4a,0)(a>0),B、C两点分别在y轴和x轴上运动,并且满足$\overrightarrow{AB}$•$\overrightarrow{BQ}$=0,$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{CQ}$.