题目内容
用余弦定理证明,平行四边形两条对角线平方的和等于四条边平方的和.
考点:余弦定理
专题:解三角形
分析:先画出平行四边形ABCD,设AB=a、AD=b,∠DAB=θ,利用余弦定理求出BD2和AC2,再由平行四边形的性质和诱导公式进行化简后,再化简AC2+BD2即可.
解答:
解:如图:平行四边形ABCD,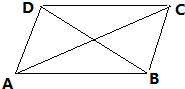 设AB=a、AD=b,∠DAB=θ,
设AB=a、AD=b,∠DAB=θ,
因为四边形ABCD是平行四边形,
所以CD=AB=a,BC=AD=b,∠ADC=180°-θ,
在△ABD中,由余弦定理得,
BD2=AB2+AD2-2AB•ADcos∠DAB
=a2+b2-2abcosθ,
在△ABD中,由余弦定理得,
AC2=DC2+AD2-2DC•ADcos∠CDA
=a2+b2-2abcos(180°-θ)=a2+b2+2abcosθ,
所以AC2+BD2=(a2+b2-2abcosθ)+(a2+b2+2abcosθ)
=2(a2+b2)=2(AB2+AD2),
即AC2+BD2=AB2+AD2+DC2+AD2,
故平行四边形两条对角线平方的和等于四条边平方的和.
 设AB=a、AD=b,∠DAB=θ,
设AB=a、AD=b,∠DAB=θ,因为四边形ABCD是平行四边形,
所以CD=AB=a,BC=AD=b,∠ADC=180°-θ,
在△ABD中,由余弦定理得,
BD2=AB2+AD2-2AB•ADcos∠DAB
=a2+b2-2abcosθ,
在△ABD中,由余弦定理得,
AC2=DC2+AD2-2DC•ADcos∠CDA
=a2+b2-2abcos(180°-θ)=a2+b2+2abcosθ,
所以AC2+BD2=(a2+b2-2abcosθ)+(a2+b2+2abcosθ)
=2(a2+b2)=2(AB2+AD2),
即AC2+BD2=AB2+AD2+DC2+AD2,
故平行四边形两条对角线平方的和等于四条边平方的和.
点评:本题考查余弦定理,诱导公式,以及平行四边形的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
cos
π=( )
| 65 |
| 6 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知数列{an}中,有an+1=an+4,且a1+a4=14.
(1)求{an}的通项公式an与前n项和公式Sn;
(2)令bn=
,若{bn}是等差数列,求数列{
}的前n项和Tn.
(1)求{an}的通项公式an与前n项和公式Sn;
(2)令bn=
| Sn |
| n+k |
| 1 |
| bnbn+1 |
将函数y=sin(2x+
)的图象沿x轴向左平移m(m>0)个单位后,得到一个奇函数的图象,则m的最小值为( )
| π |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
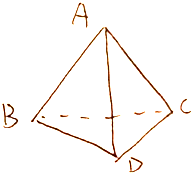 如图三棱锥A-BCD中DC⊥BC,BC=2
如图三棱锥A-BCD中DC⊥BC,BC=2
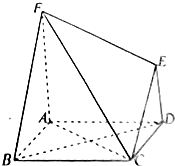 在如图所示的多面体ABCDEF中,四边形ABCD是正方形,AF⊥平面ABCD,DE⊥平面ABCD,且AF=2DE
在如图所示的多面体ABCDEF中,四边形ABCD是正方形,AF⊥平面ABCD,DE⊥平面ABCD,且AF=2DE