题目内容
14.执行如图所示的程序框图,则输出S的值是( )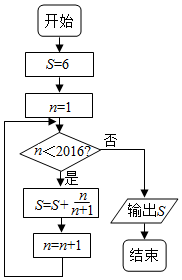
| A. | 336 | B. | $\frac{1}{336}$ | C. | 2016 | D. | $\frac{1}{2016}$ |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算并输出S=6×$\frac{1}{2}×\frac{2}{3}×$…×$\frac{2015}{2016}$的值,从而计算得解.
解答 解:模拟执行程序框图,可得该程序的作用是计算并输出:S=6×$\frac{1}{2}×\frac{2}{3}×$…×$\frac{2015}{2016}$的值,
由于:S=6×$\frac{1}{2}×\frac{2}{3}×$…×$\frac{2015}{2016}$=$\frac{6}{2016}$=$\frac{1}{336}$,
故选:B.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.

练习册系列答案
相关题目
4.已知函数f(x)=$\left\{\begin{array}{l}{2x,(x≤\frac{1}{2})}\\{2-2x,(x>\frac{1}{2})}\end{array}\right.$,则函数$\underset{\underbrace{f(f(…f(x)…))}}{2015}$在[0,1]上的图象总长( )
| A. | 8060 | B. | 4030 | C. | 2015$\sqrt{5}$ | D. | $\sqrt{{2^{4030}}+1}$ |
9.执行下面的程序框图,如果输入的t=0.01,则输出的n=( )


| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
19.某地植被面积 x(公顷)与当地气温下降的度数y(℃)之间有如下的对应数据:
(1)请用最小二乘法求出y关于x的线性回归方程$\widehaty=\hat bx+\hat a$;
(2)根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少℃?
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}{y}_{i})-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| x(公顷) | 20 | 40 | 50 | 60 | 80 |
| y(℃) | 3 | 4 | 4 | 4 | 5 |
(2)根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少℃?
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}{y}_{i})-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
4.6名同学排成一排,则甲乙恰好相邻排在一起的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{6}$ |