题目内容
4．6名同学排成一排，则甲乙恰好相邻排在一起的概率为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{6}$ |
分析 6名同学排成一排，先求出基本事件总数，再求出甲乙恰好相邻排在一起包含的基本事件个数，由此能求出甲乙恰好相邻排在一起的概率．
解答 解：6名同学排成一排，
基本事件总数n=${A}_{6}^{6}$=720．
甲乙恰好相邻排在一起包含的基本事件个数m=${A}_{2}^{2}{A}_{5}^{5}$=240，
∴甲乙恰好相邻排在一起的概率p=$\frac{240}{720}$=$\frac{1}{3}$．
故选：A．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
相关题目
14．执行如图所示的程序框图，则输出S的值是（ ）
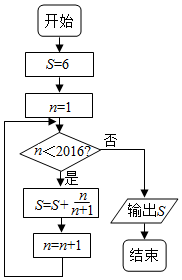
| A． | 336 | B． | $\frac{1}{336}$ | C． | 2016 | D． | $\frac{1}{2016}$ |
12．已知a1=$\frac{1}{lo{g}_{9}3}$，数列{$\frac{1}{2}$an+3}是公比为$\frac{1}{2}$的等比数列，则a8=（ ）
| A． | $\frac{191}{32}$ | B． | -$\frac{191}{32}$ | C． | $\frac{95}{16}$ | D． | -$\frac{95}{16}$ |
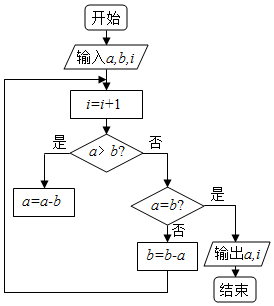如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b，i的值分别为12，16，0，则输出a和i的值分别为（ ）