题目内容
2.在数列{an}中,a1=1,且对于任意自然数n,都有an+1=an+n,则a6=16.分析 由条件可得an+1-an=n,利用叠加法,即可得到结论.
解答 解:∵an+1=an+n,∴an+1-an=n,
∴an=a1+(a2-a1)+…+(an-an-1)=1+1+2+…+(n-1)=1+$\frac{n(n+1)}{2}$
∴a6=1+$\frac{6×(6-1)}{2}$=16,
故答案为:16.
点评 本题考查数列的求和,考查叠加法的运用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.设$a={log}_{\frac{2}{5}}2,b={(\frac{1}{2})}^{\frac{1}{5}},c={2}^{\frac{2}{5}}$,则a,b,c的大小关系是( )
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>c>a |
14.执行如图所示的程序框图,则输出S的值是( )
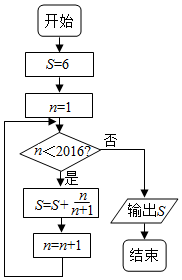

| A. | 336 | B. | $\frac{1}{336}$ | C. | 2016 | D. | $\frac{1}{2016}$ |
12.已知a1=$\frac{1}{lo{g}_{9}3}$,数列{$\frac{1}{2}$an+3}是公比为$\frac{1}{2}$的等比数列,则a8=( )
| A. | $\frac{191}{32}$ | B. | -$\frac{191}{32}$ | C. | $\frac{95}{16}$ | D. | -$\frac{95}{16}$ |
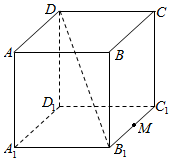 如图AC1是棱长为2的正方体,M为B1C1的中点,给出下列命题:
如图AC1是棱长为2的正方体,M为B1C1的中点,给出下列命题: