题目内容
19.某地植被面积 x(公顷)与当地气温下降的度数y(℃)之间有如下的对应数据:| x(公顷) | 20 | 40 | 50 | 60 | 80 |
| y(℃) | 3 | 4 | 4 | 4 | 5 |
(2)根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少℃?
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}{y}_{i})-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
分析 (1)先求出五对数据的平均数,求出年份和人口数的平均数,得到样本中心点,把所给的数据代入公式,利用最小二乘法求出线性回归方程的系数,再求出a的值,从而得到线性回归方程.
(2)(2)把当x=200时,代入线性回归方程,得到8.5°C,即下降的气温大约是多少8.5°C.
解答 解:(1)$\overline x=\frac{20+40+50+60+80}{5}=50$,$\overline y=\frac{3+4+4+4+5}{5}=4$.$\sum_{i=1}^5{{x_i}{y_i}}=20×3+40×4+50×4+60×4+80×5=1060$,$\sum_{i=1}^5{{x_i}^2}={20^2}+{40^2}+{50^2}+{60^2}+{80^2}=14500$.
所以 $\hat b=\frac{1060-5×50×4}{{14500-5×{{50}^2}}}=0.03$,$\hat a=4-0.03×50=2.5$.
故y关于x的线性回归方程$\widehaty=0.03x+2.5$.
(2)由(1)得:当x=200时,$\widehaty=0.03×200+2.5=8.5$.
所以植被面积为200公顷时,下降的气温大约是8.5°C.
点评 本题考查线性回归方程,考查最小二乘法,考查预报值的求法,是一个新课标中出现的新知识点,已经在广东的高考卷中出现过类似的题目,属于基础题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
9.双曲线2x2-y2=1的渐近线方程是( )
| A. | y=±$\frac{1}{2}$x | B. | y=±2x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\sqrt{2}$x |
10.设$a={log}_{\frac{2}{5}}2,b={(\frac{1}{2})}^{\frac{1}{5}},c={2}^{\frac{2}{5}}$,则a,b,c的大小关系是( )
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>c>a |
14.执行如图所示的程序框图,则输出S的值是( )
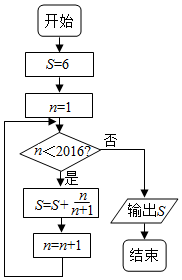

| A. | 336 | B. | $\frac{1}{336}$ | C. | 2016 | D. | $\frac{1}{2016}$ |
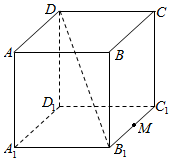 如图AC1是棱长为2的正方体,M为B1C1的中点,给出下列命题:
如图AC1是棱长为2的正方体,M为B1C1的中点,给出下列命题: