题目内容
求函数f(x)=x(a-x),x∈[-1,1]的最大值为g(a),并作出g(a)的图象.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:由条件利用二次函数的性质分类讨论求得函数在区间[-1,1]上的最大值g(a)的解析式,综合可得结论.
解答:
 解:函数f(x)=x(a-x)的图象是开口向下的抛物线,对称轴方程为x=
解:函数f(x)=x(a-x)的图象是开口向下的抛物线,对称轴方程为x=
,在区间[-1,1]上,
当
<-1时,函数在区间[-1,1]上是减函数,最大值g(a)=f(-1)=-a-1.
当
∈[-1,1]时,最大值g(a)=f(
)=
.
当
>1时,函数在区间[-1,1]上是增函数,最大值g(a)=f(1)=a-1.
综上可得,g(a)=
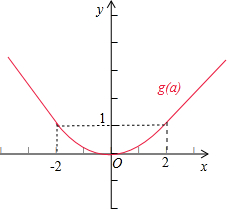
,如图所示:
 解:函数f(x)=x(a-x)的图象是开口向下的抛物线,对称轴方程为x=
解:函数f(x)=x(a-x)的图象是开口向下的抛物线,对称轴方程为x=| a |
| 2 |
当
| a |
| 2 |
当
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
当
| a |
| 2 |
综上可得,g(a)=
|
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等差数列{an}的公差和首项都不等于0,且a2、a4、a8成等比数列,则下列式子的值最小的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|