题目内容
已知sin(45°+α)sin(45°-α)=-
,(0°<α<90°).
(1)求α的值;
(2)求sin(α+10°)[1-
tan(α-10°)]的值.
| 1 |
| 4 |
(1)求α的值;
(2)求sin(α+10°)[1-
| 3 |
考点:两角和与差的正弦函数,三角函数的化简求值
专题:三角函数的求值
分析:(1)利用诱导公式把sin(45°-α)转化为cos(45°+α),进而利用二倍角公式化简求得cos2α,则α的值可得.
(2)把(1)中α的值带入,进而把切转化成弦,利用诱导公式和二倍角公式化简.
(2)把(1)中α的值带入,进而把切转化成弦,利用诱导公式和二倍角公式化简.
解答:
解:(1)sin(45°+α)sin(45°-α)=sin(45°+α)cos(45°+α)=
sin(90°+2α)=-
,
∴cos2α=-
,
∵0°<α<90°,
∴0°<2α<180°,
∴2α=120°,α=60°.
(2)原式=sin70°(1-
tan50°)=sin70°×
=sin70°×
=
=
=-
=-1.
| 1 |
| 2 |
| 1 |
| 4 |
∴cos2α=-
| 1 |
| 2 |
∵0°<α<90°,
∴0°<2α<180°,
∴2α=120°,α=60°.
(2)原式=sin70°(1-
| 3 |
cos50°-
| ||
| cos50° |
| 2cos110° |
| cos50° |
| -2sin70°cos70° |
| cos50° |
| -sin140° |
| cos50° |
| cos50° |
| cos50° |
点评:本题主要考查了考查了二倍角公式和两角和公式的化简求值.考查了学生对三角函数基础知识的灵活运用.

练习册系列答案
相关题目
若直线l1,l2的方向向量分别为
=(2,4,-4),
=(-6,9,6),则( )
| a |
| b |
| A、l1∥l2 |
| B、l1⊥l2 |
| C、l1与l2相交但不垂直 |
| D、以上均不正确 |
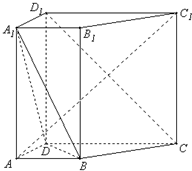 如图,在直四棱柱ANCD-A1B1C1D1中,已知DC=DD1=2AD=2AB=2,AD⊥DC,AB∥DC.
如图,在直四棱柱ANCD-A1B1C1D1中,已知DC=DD1=2AD=2AB=2,AD⊥DC,AB∥DC.