题目内容
9.已知抛物线y2=4x的过焦点的弦AB被焦点分成长为d1、d2的两段,那么( )| A. | d1+d2=d1•d2 | B. | d1-d2=d1•d2 | C. | d12+d22=d1•d2 | D. | d12-d22=d1•d2 |
分析 求出抛物线的焦点F(1,0),准线x=-1,再设y=k(x-1)代入y2=4x得k2x2-2(k2+2)x+k2=0,由抛物线定义可得|AF|=x1+1,|BF|=x2+1,从而可得结论.
解答 解:抛物线的焦点F(1,0),准线x=-1,
设y=k(x-1),把它代入y2=4x得k2x2-2(k2+2)x+k2=0,
设A(x1,y1),B(x2,y2),则x1x2=1
由抛物线定义可得|AF|=x1+1,|BF|=x2+1,
∴d1+d2=(x1+1)+(x2+1)=(x1+x2)+2,d1d2=(x1+1)(x2+1)=x1x2+(x1+x2)+1=(x1+x2)+2
∴d1+d2=d1d2.
故选:A.
点评 本题考查抛物线过焦点的性质,解题的关键是设出过焦点的直线方程与抛物线方程联立方程组.

练习册系列答案
相关题目
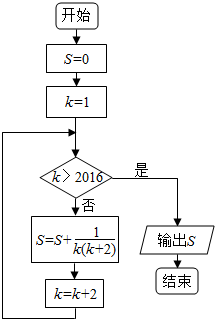
20.执行下列程序框图,则输出结果为( )


| A. | 413 | B. | 404 | C. | 397 | D. | 407 |
17.如图程序框图表示的算法是:求1+2+3+4+…+n>20时n的最小值,则输出框中应填( )


| A. | i | B. | i+1 | C. | i-1 | D. | n |
4.在△ABC中,角A为钝角,AB=3,$\overrightarrow{BC}$•$\overrightarrow{BA}$=12,当角C最大时,△ABC的面积等于( )
| A. | 2 | B. | 3 | C. | 5 | D. | $\frac{15}{2}$ |
2.若a<0<b,则下列不等式恒成立的是( )
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | -a>b | C. | a2>b2 | D. | a3<b3 |