��Ŀ����
11����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����ԲC�ij����᳤Ϊ2����1������ԲC�ķ��̣�
��2����ֱ֪��l��y=kx-$\sqrt{3}$����ԲC����A��B���㣬�Ƿ����ʵ��kʹ�����߶�ABΪֱ����Բǡ�þ�������ԭ��O�������ڣ����k��ֵ���������ڣ���˵�����ɣ�
���� ��1������Բ�Ľ����Ϊc���������裬��$\left\{{\begin{array}{l}{a=2}\\{\frac{c}{a}=\frac{{\sqrt{3}}}{2}}\end{array}}\right.$�������ԲC�ļ�������Ȼ�������Բ���̣�
��2������ʵ��kʹ�����߶�ABΪֱ����Բǡ�þ�������ԭ��O���������£����A��x1��y1����B��x2��y2������ֱ��l�ķ���$y=kx-\sqrt{3}$����$\frac{x^2}{4}+{y^2}=1$������Τ�ﶨ���Լ���������������ת����⼴�ɣ�
��� ��1������Բ�Ľ����Ϊc���������裬��$\left\{{\begin{array}{l}{a=2}\\{\frac{c}{a}=\frac{{\sqrt{3}}}{2}}\end{array}}\right.$�����$\left\{{\begin{array}{l}{a=2}\\{c=\sqrt{3}}\end{array}}\right.$������2�֣�
����b2=a2-c2=4-3=1����������ԲC�ķ���Ϊ$\frac{x^2}{4}+{y^2}=1$����..��4�֣�
��2������ʵ��kʹ�����߶�ABΪֱ����Բǡ�þ�������ԭ��O���������£�
���A��x1��y1����B��x2��y2������ֱ��l�ķ���$y=kx-\sqrt{3}$����$\frac{x^2}{4}+{y^2}=1$��
����������$��1+4{k^2}��{x^2}-8\sqrt{3}x+8=0$����*��������6�֣�
��${x_1}+{x_2}=\frac{{8\sqrt{3}k}}{{1+4{k^2}}}$��${x_1}{x_2}=\frac{8}{{1+4{k^2}}}$������8�֣�
��Ϊ���߶�ABΪֱ����Բǡ�þ�������ԭ��O������$\overrightarrow{OA}•\overrightarrow{OB}=0$����x1x2+y1y2=0��
��${y_1}{y_2}={k^2}{x_1}{x_2}-\sqrt{3}k��{x_1}+{x_2}��+3$������$\frac{8}{{1+4{k^2}}}-\frac{{4{k^2}-3}}{{1+4{k^2}}}=0$��������10�֣�
���$k=��\frac{{\sqrt{11}}}{2}$����..��11�֣�
������֪����ʱ��*��ʽ�ġ���0���������⣮
���Ե�$k=��\frac{{\sqrt{11}}}{2}$ʱ�����߶�ABΪֱ����Բǡ�þ�������ԭ��O������12�֣�
���� ���⿼����Բ���̵���ֱ������Բ��λ�ù�ϵ���ۺ�Ӧ�ã��������������Ĵ����������������������

 ��У����ϵ�д�
��У����ϵ�д�| �۸�x��Ԫ/kg�� | 10 | 15 | 20 | 25 | 30 |
| ��������y��kg�� | 11 | 10 | 8 | 6 | 5 |
��2�����ã�1���еĻع鷽�̣����۸�x=40Ԫ/kgʱ����������y��Ԥ��ֵΪ���٣�
�ο���ʽ�����Իع鷽��y=bx+a������b=$\frac{{x}_{1}{y}_{1}+{x}_{2}{y}_{2}+��{x}_{n}{y}_{n}-n\overline{x}\overline{y}}{{{x}_{1}}^{2}+{{x}_{2}}^{2}+��{{x}_{n}}^{2}-n{\overline{x}}^{2}}$��a=$\overline{y}$-b$\overline{x}$��
| A�� | ��Ҫ��������� | B�� | ��ֲ���Ҫ���� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
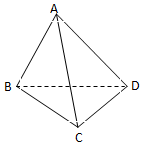 ��ͼ��������A-BCD�У���֪����BAC=60�㣬BD=DC=$\sqrt{2}$��AB=AC=AD=2��
��ͼ��������A-BCD�У���֪����BAC=60�㣬BD=DC=$\sqrt{2}$��AB=AC=AD=2��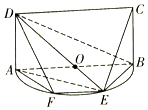 ��ͼ����ԲO��ֱ��AB��Ϊ2��E�ǰ�ԲO�ϳ�A��B���һ�����㣬����ABCD���ڵ�ƽ�洹ֱ�ڸð�Բ���ڵ�ƽ�棬��$tan��DBA=\frac{1}{2}$����ƽ��ECD���Բ������һ������ΪF��
��ͼ����ԲO��ֱ��AB��Ϊ2��E�ǰ�ԲO�ϳ�A��B���һ�����㣬����ABCD���ڵ�ƽ�洹ֱ�ڸð�Բ���ڵ�ƽ�棬��$tan��DBA=\frac{1}{2}$����ƽ��ECD���Բ������һ������ΪF��