题目内容
13．已知某圆与y轴切于点（0，3），与x轴所截得的线段长为8，则该圆的标准方程为（x+5）2+（y-3）2=25或（x-5）2+（y-3）2=25．分析 根据题意，设圆的圆心为（a，3），分析可得其半径r=|a|，又由该圆与x轴所截得的线段长为8，分析有r2=（$\frac{8}{2}$）2+32=25，即可得圆的半径以及圆心坐标，将其代入圆的标准方程即可得答案．
解答 解：根据题意，已知圆与y轴切于点（0，3），
则设圆的圆心为（a，3），则其半径r=|a|，
又由该圆与x轴所截得的线段长为8，则有r2=（$\frac{8}{2}$）2+32=25，
即r=5，
则a=±5，
故圆的方程为（x+5）2+（y-3）2=25或（x-5）2+（y-3）2=25．
点评 本题考查圆的标准方程，注意要根据题意，分析圆的圆心与半径的关系．
练习册系列答案
相关题目
9．设x，y满足约束条件$\left\{\begin{array}{l}8x-y-4≤0\\ x+y+1≥0\\ y-4x≤0\end{array}\right.$，目标函数z=ax+by（a＞0，b＞0）的最大值为2，则$\frac{1}{a}+\frac{1}{b}$的最小值为（ ）
| A． | 5 | B． | $\frac{5}{2}$ | C． | $\frac{9}{2}$ | D． | 9 |
4．已知实数x、y满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y≥0\\ x≤1\end{array}\right.$，则z=2x-y的最小值是（ ）
| A． | -1 | B． | 1 | C． | -3 | D． | 2 |
1．某种商品价格与该商品日需求量之间的几组对照数据如表：
（1）求y关x的线性回归方程；
（2）利用（1）中的回归方程，当价格x=40元/kg时，日需求量y的预测值为多少？
参考公式：线性回归方程y=bx+a，其中b=$\frac{{x}_{1}{y}_{1}+{x}_{2}{y}_{2}+…{x}_{n}{y}_{n}-n\overline{x}\overline{y}}{{{x}_{1}}^{2}+{{x}_{2}}^{2}+…{{x}_{n}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$．
| 价格x（元/kg） | 10 | 15 | 20 | 25 | 30 |
| 日需求量y（kg） | 11 | 10 | 8 | 6 | 5 |
（2）利用（1）中的回归方程，当价格x=40元/kg时，日需求量y的预测值为多少？
参考公式：线性回归方程y=bx+a，其中b=$\frac{{x}_{1}{y}_{1}+{x}_{2}{y}_{2}+…{x}_{n}{y}_{n}-n\overline{x}\overline{y}}{{{x}_{1}}^{2}+{{x}_{2}}^{2}+…{{x}_{n}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$．
8．已知圆心为（2，-3），一条直径的两个端点恰好在两个坐标轴上，则圆的方程是（ ）
| A． | （x-2）2+（y+3）2=5 | B． | （x-2）2+（y+3）2=21 | C． | （x-2）2+（y+3）2=13 | D． | （x-2）2+（y+3）2=52 |
18．用反证法证明命题：“若正系数一元二次方程ax2+bx+c=0（a=0）有有理根，那么a，b，c中至多有两个是奇数”时，下列假设中正确的是（ ）
| A． | 假设a，b，c都是奇数 | B． | 假设a，b，c至少有两个是奇数 | ||
| C． | 假设a，b，c至多有一个是奇数 | D． | 假设a，b，c不都是奇数 |
已知定义在[-2，2]上的函数y=f（x）和 y=g（x），其图象如图所示：给出下列四个命题：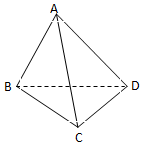
如图，在三棱锥A-BCD中，已知，∠BAC=60°，BD=DC=$\sqrt{2}$，AB=AC=AD=2．