题目内容
已知数列{an}中,a1=2,an-an-1-2n=0,(n≥2,n∈N).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
+
+
+…+
,求数列{bn}的通项公式.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| an+3 |
| 1 |
| a2n |
考点:数列递推式,数列的求和
专题:综合题,等差数列与等比数列
分析:(Ⅰ)利用叠加法,即可求数列{an}的通项公式;
(Ⅱ)利用裂项法,可求数列{bn}的通项公式.
(Ⅱ)利用裂项法,可求数列{bn}的通项公式.
解答:
解:(Ⅰ)∵a1=2,an-an-1-2n=0(n≥2,n∈N)
∴当n≥2时,an-an-1=2n,an-1-an-2=2(n-1),…,a3-a2=2×3,a2-a1=2×2,
∴an-a1=2[n+(n-1)+…+3+2],
∴an=2[n+(n-1)+…+3+2+1]=2
=n(n+1)
当n=1时,a1=1×(1+1)=2也满足上式,
∴数列{an}的通项公式为an=n(n+1)
(Ⅱ)bn=
+
+…+
=
+
+…+
=
-
+
-
+…+
-
=
-
=
∴当n≥2时,an-an-1=2n,an-1-an-2=2(n-1),…,a3-a2=2×3,a2-a1=2×2,
∴an-a1=2[n+(n-1)+…+3+2],
∴an=2[n+(n-1)+…+3+2+1]=2
| n(n+1) |
| 2 |
当n=1时,a1=1×(1+1)=2也满足上式,
∴数列{an}的通项公式为an=n(n+1)
(Ⅱ)bn=
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| a2n |
| 1 |
| (n+1)(n+2) |
| 1 |
| (n+2)(n+3) |
| 1 |
| 2n(2n+1) |
=
| 1 |
| (n+1) |
| 1 |
| (n+2) |
| 1 |
| (n+2) |
| 1 |
| (n+3) |
| 1 |
| 2n |
| 1 |
| (2n+1) |
| 1 |
| (n+1) |
| 1 |
| (2n+1) |
| n |
| 2n2+3n+1 |
点评:本题考查数列的通项与求和,正确运用叠加法、裂项法是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
已知全集U=R,集合A={y|y≥1},B=(-∞,-1)∪(2,+∞),则A∪(∁UB)=( )
| A、[1,2] |
| B、[1,+∞) |
| C、[-1,+∞) |
| D、(-∞,-1]∪[1,+∞) |
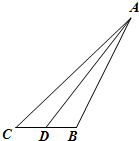 如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cosα=-
如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cosα=-