题目内容
1.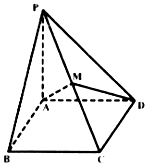 已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.
已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.(Ⅰ)在图中作出平面ADM与PB的交点N,并指出点N所在位置(不要求给出理由);
(Ⅱ)在线段CD上是否存在一点E,使得直线AE与平面ADM所成角的正弦值为$\frac{\sqrt{10}}{10}$,若存在,请说明点E的位置;若不存在,请说明理由;
(Ⅲ)求二面角A-MD-C的余弦值.
分析 (Ⅰ)过M作MN∥BC,交PB于点N,由此求出结果.
(Ⅱ)以A为坐标原点,以直线AB,AD,AP所在直线建立空间直角坐标系,利用向量法能求出在线段CD上存在中点E,使得直线AE与平面AMD所成角的正弦值为$\frac{{\sqrt{10}}}{10}$.
(Ⅲ)求出平面CMD的法向量和平面AMD的法向量,由此利用向量法能求出二面角A-MD-C的平面角的余弦值.
解答 解:(Ⅰ)过M作MN∥BC,交PB于点N,连接AN,如图,
则点N为平面ADM与PB的交点N(在图中画出)
由M为PC中点,得N为PB的中点.…(2分)
(Ⅱ)因为四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,
以A为坐标原点,以直线AB,AD,AP所在直线建立空间直角坐标系如图所示:
则A(0,0,0),P(0,0,1),D(0,1,0),C(2,1,0),M(1,$\frac{1}{2},\frac{1}{2}$),…(4分)
设在线段CD上存在一点E(x,1,0),则$\overrightarrow{AE}=(x,1,0)$…(5分)
设直线AE与平面AMD所成角为θ,平面AMD的法向量为$\overrightarrow u=(x,y,z)$,
则$\overrightarrow u⊥\overrightarrow{AM},\overrightarrow u⊥\overrightarrow{AD}$,即$\left\{\begin{array}{l}x+\frac{1}{2}y+\frac{1}{2}z=0\\ y=0\end{array}\right.$,令z=2,则$\overrightarrow u=(-1,0,2)$,…(7分)
因为直线AE与平面ADM所成角的正弦值为$\frac{\sqrt{10}}{10}$,
所以$sinθ=\frac{{|\overrightarrow{AE}•\overrightarrow u|}}{{|\overrightarrow{AE}||\overrightarrow u|}}=\frac{{\sqrt{10}}}{10}$,所以x=1
所以在线段CD上存在中点E,
使得直线AE与平面AMD所成角的正弦值为$\frac{{\sqrt{10}}}{10}$…(8分)
(Ⅲ)设平面CMD的法向量$\overrightarrow v=({x^'},{y^'},{z^'})$,
则$\overrightarrow v⊥\overrightarrow{CM},\overrightarrow v⊥\overrightarrow{CD}$,即$\left\{\begin{array}{l}-{x^'}-\frac{1}{2}{y^'}+\frac{1}{2}{z^'}=0\\-2{x^'}=0\end{array}\right.$,令z′=-1,则y′=-1,
所以$\overrightarrow v=(0,-1,-1)$….…(10分)
所以$cosϕ=\frac{\overrightarrow v•\overrightarrow u}{|\overrightarrow v||\overrightarrow u|}=-\frac{{\sqrt{10}}}{5}$,
由图形知二面角A-MD-C的平面角是钝角,
所以二面角A-MD-C的平面角的余弦值为$-\frac{{\sqrt{10}}}{5}$…..…(12分)
点评 本题考查线面交点的作法,考查满足线面角正弦值的点是否存在的判断与求法,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | (0,2) | B. | (-2,0) | C. | {1,2} | D. | {1} |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
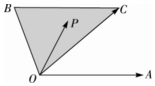 已知图中∠AOC+2∠BOC=π,|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|,BC∥OA,P为图中的阴影中(含边界)任意点,并且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$,下列正确的是①③⑤
已知图中∠AOC+2∠BOC=π,|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|,BC∥OA,P为图中的阴影中(含边界)任意点,并且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$,下列正确的是①③⑤ 如图,已知三棱锥A-OCB中,AO⊥底面BOC,且∠BAO=∠CAO=$\frac{π}{6}$,AB=4,点D为线段AB的中点,记二面角B-AO-C的大小为θ.
如图,已知三棱锥A-OCB中,AO⊥底面BOC,且∠BAO=∠CAO=$\frac{π}{6}$,AB=4,点D为线段AB的中点,记二面角B-AO-C的大小为θ.