题目内容

若关于x的方程9x-（4+a）•3x+4=0有解，则实数a的取值范围是
 
．
考点：根的存在性及根的个数判断
专题：计算题,函数的性质及应用
分析：可分离出a+4，利用基本不等式和不等式的性质即可求出实数a的取值范围．
解答： 解：∵9x-（4+a）•3x+4=0，
∴a+4=3x+
4
3x
≥2
3x•
4
3x
=4，
∴a≥0，
所以a的范围为[0，+∞）
故答案为[0，+∞）．
点评：本题考查指数函数的定义、基本不等式求最值问题，同时考查转化思想，比较基础．
练习册系列答案
相关题目
已知在平行六面体ABCD-A1B1C1D1中．
（1）AB=AD=AA1=1，且∠A1AD=∠A1AB=∠DAB=
π
3
，求AC1的长；
（2）底面ABCD是菱形，∠A1AD=∠A1AB=∠DAB=θ，当
AA1
AB
为何值时，AC1⊥面A1BD．
偶函数f（x）满足f（x-1）=f（x+1），且在x∈[0，1]时，f（x）=x2，g（x）=ln|x|，则函数f（x）与g（x）图象交点的个数是（　　）
A、1B、2C、3D、4
已知数列{an}中，a1=1，an+1=
an
1+3an
，求{an}的通项公式．
已知集合A={x丨x2+ax-1=0}，4∈A，则a的值
 
．
已知圆方程为y2-6ysinθ+x2-8xcosθ+7cos2θ+8=0．
①求圆心轨迹的参数方程C；
②点P（x，y）是①中曲线C上的动点，求2x+y的取值范围．
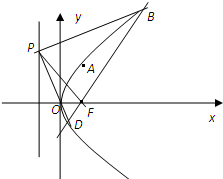在平面直角坐标系xOy中，抛物线C的顶点在原点，经过点A（1，2）其焦点F在x轴上．
（Ⅰ）求抛物线C的标准方程；
（Ⅱ）求过点F和OA的中点的直线的方程；
（Ⅲ）设点P（-1，m），过点F的直线交抛物线C于B、D两点，记PB，PF，PD的斜率分别为k1，k2，k3，求证：k1+k3=2k2．
若数列{bn}满足：对于n∈N*，都有bn+2-bn=d（d为常数），则称数列{bn}是公差为d的“隔项等差”数列．
（Ⅰ）若c1=3，c2=17，{cn}是公差为8的“隔项等差”数列，求{cn}的前15项之和；
（Ⅱ）设数列{an}满足：a1=a，对于n∈N*，都有an+an+1=2n．
①求证：数列{an}为“隔项等差”数列，并求其通项公式；
②设数列{an}的前n项和为Sn，试研究：是否存在实数a，使得S2k，S2k+1，S2k+2成等比数列（k∈N*）？若存在，请求出a的值；若不存在，请说明理由．
已知函数f（x）=x2-（a+2）x+alnx，当常数a＞2时，函数f（x）的单调递增区间为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网