题目内容
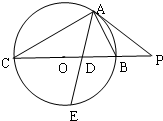如图，△ABC内接于直径为F1，F2的圆P，过点A作圆O的切线交CB的延长线于点P，∠BAC的平分线分别交BC和圆O于点D、E，若PA=2PB=10（1）求证：AC=2AB；
（2）求AD•DE的值．
考点：与圆有关的比例线段,相似三角形的判定
专题：直线与圆,推理和证明
分析：（1）由弦切角定理推导出△ABP∽△CAP，由此能证明AC=2AB．
（2）由切割线定理得：PA2=PB•PC，从而PC=20，BC=15，由AD是∠BAC的平分线，得CD=10，DB=5，再由相交弦定理得：AD•DE=CD•DB=50．
（2）由切割线定理得：PA2=PB•PC，从而PC=20，BC=15，由AD是∠BAC的平分线，得CD=10，DB=5，再由相交弦定理得：AD•DE=CD•DB=50．
解答：
（1）证明：∵PA是圆O的切线，∴∠PAB=∠ACB，又∠P是公共角
∴△ABP∽△CAP，…（2分）
∴
=
=2，∴AC=2AB．…（4分）
（2）解：由切割线定理得：PA2=PB•PC，
∴PC=20，又PB=5，∴BC=15，…（6分）
又∵AD是∠BAC的平分线，
∴
=
=2，
∴CD=2DB，∴CD=10，DB=5…（8分）
又由相交弦定理得：AD•DE=CD•DB=50．…（10分）
∴△ABP∽△CAP，…（2分）
∴
| AC |
| AB |
| AP |
| PB |
（2）解：由切割线定理得：PA2=PB•PC，
∴PC=20，又PB=5，∴BC=15，…（6分）
又∵AD是∠BAC的平分线，
∴
| AC |
| AB |
| CD |
| DB |
∴CD=2DB，∴CD=10，DB=5…（8分）
又由相交弦定理得：AD•DE=CD•DB=50．…（10分）
点评：本题考查一线段长是另一线段长的2倍的证明，考查两线段乘积的求法，是中档题，解题时要认真审题，注意弦切角定理、切割线定理、相交弦定理的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f（x）（x∈R）满足f′（x）＞f（x），则（ ）
| A、f（1）＞ef（0）＞e2f（-1） |
| B、f（1）＜ef（0）＜e2f（-1） |
| C、e2f（-1）＞ef（0）＞f（1） |
| D、e2f（-1）＜ef（0）＜f（1） |
一个几何体的三视图如图所示，则该几何体的体积为（ ）
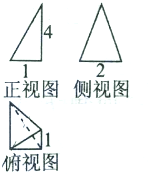
| A、2 | ||||
B、
| ||||
C、
|
如图，已知Rt△ABC的两条直角边AC，BC的长分别为6cm，8cm，以AC为直径的圆与AB交于点D则BD=四棱锥的三视图如图所示，则最长的一条侧棱的长度是（ ）
A、
| ||
| B、5 | ||
C、
| ||
D、2
|