题目内容
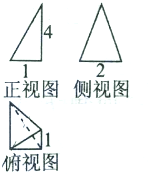
一个几何体的三视图如图所示，则该几何体的体积为（ ）
| A、2 | ||||
B、
| ||||
C、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图可判断几何体为四棱锥，底面为梯形，上底长为1，下底长为2，高为1，棱锥的高为4，代入公式可求体积．
解答：
解：由三视图知几何体为四棱锥，底面为梯形，上底长为1，下底长为2，高为1，棱锥的高为4
所以体积V=
×
×1×4=2
故选：A．
所以体积V=
| 1 |
| 3 |
| 1+2 |
| 2 |
故选：A．
点评：本题考查由三视图求几何体的体积问题，解题的关键是由三视图判断几何体的相关元素的数据．
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
在等差数列{an}中，若a2=1，a8=2a6+a4，则a5的值是（ ）
| A、-5 | ||
B、-
| ||
C、
| ||
D、
|
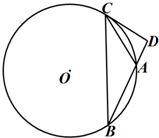
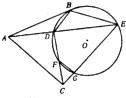如图，AB是⊙O的切线，B为切点，ADE是⊙O的割线，C是⊙O外一点，且AB=AC，连接BD，BE，CD，CE，CD交⊙O于F，CE交⊙O于G．一个几何体的三视图如图所示，则这个几何体的体积等于（ ）
| A、4 | B、6 | C、8 | D、12 |
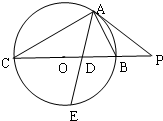如图，△ABC内接于直径为F1，F2的圆P，过点A作圆O的切线交CB的延长线于点P，∠BAC的平分线分别交BC和圆O于点D、E，若PA=2PB=10