题目内容
已知函数f(x)∈{x-1,log2|x|,x
},且f(x)为偶函数.
(1)确定函数f(x)的解析式;
(2)设函数g(x)=m•2f(x)+x2(m∈R).
①若函数g(x)在区间(-∞,-2)上是减函数,求实数m的取值范围;
②当m>
时,证明:g(x)>
x+
在x∈[1,2]上恒成立.
| 1 |
| 2 |
(1)确定函数f(x)的解析式;
(2)设函数g(x)=m•2f(x)+x2(m∈R).
①若函数g(x)在区间(-∞,-2)上是减函数,求实数m的取值范围;
②当m>
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| x |
考点:函数恒成立问题
专题:函数的性质及应用
分析:(1)根据每个函数的奇偶性确定函数f(x);
(2)①借助于二次函数的单调性性质求解;
②将不等式化简归零,而后将问题转化为函数的最值问题来解.
(2)①借助于二次函数的单调性性质求解;
②将不等式化简归零,而后将问题转化为函数的最值问题来解.
解答:
解:(1)若f(x)=x-1,则f(-x)=(-x)-1=-x-1=-f(x),所以f(x)为奇函数,不合题意;
若f(x)=x
,则f(x)的定义域为[0,+∞),所以f(x)即不是奇函数,也不是偶函数,不合题意;
若f(x)=log2|x|,则f(-x)=log2|-x|=log2|x|=f(x),所以f(x)为偶函数,符合题意,
综上可知,函数f(x)=log2|x|.
(2)g(x)=m•2log2|x|+x2.
①因为x∈(-∞,-2)时,g(x)=x2-mx.
所以,当m≥0时,g(x)在(-∞,-2)上单调递减,符合题意;
当m<0时,要使得g(x)在(-∞,-2)上单调递减,须且只须
≥-2,
即m≥-4,所以-4≤m≤0.
综上所述,所求m的取值范围是[-4,+∞).
②当x∈[1,2]时,g(x)=x2+mx.
所以g(x)>
x+
?x2+mx>
x+
?(m-
)x2-1>-x3.
令F(x)=(m-
)x2-1(1≤x≤2),G(x)=-x3(1≤x≤2).
因为m>
,所以函数F(x)在区间[1,2]上单调递增,
所以F(x)min=F(1)=m-
>
-
=-1,所以F(x)>-1,
又因为函数G(x)在区间[1,2]上单调递减,
所以G(x)max=G(1)=-1,所以G(x)≤-1,
所以F(x)>G(x),
所以G(x)>
x+
在x∈[1,2]上恒成立.
若f(x)=x
| 1 |
| 2 |
若f(x)=log2|x|,则f(-x)=log2|-x|=log2|x|=f(x),所以f(x)为偶函数,符合题意,
综上可知,函数f(x)=log2|x|.
(2)g(x)=m•2log2|x|+x2.
①因为x∈(-∞,-2)时,g(x)=x2-mx.
所以,当m≥0时,g(x)在(-∞,-2)上单调递减,符合题意;
当m<0时,要使得g(x)在(-∞,-2)上单调递减,须且只须
| m |
| 2 |
即m≥-4,所以-4≤m≤0.
综上所述,所求m的取值范围是[-4,+∞).
②当x∈[1,2]时,g(x)=x2+mx.
所以g(x)>
| 1 |
| 4 |
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| x |
| 1 |
| 4 |
令F(x)=(m-
| 1 |
| 4 |
因为m>
| 1 |
| 4 |
所以F(x)min=F(1)=m-
| 5 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
又因为函数G(x)在区间[1,2]上单调递减,
所以G(x)max=G(1)=-1,所以G(x)≤-1,
所以F(x)>G(x),
所以G(x)>
| 1 |
| 4 |
| 1 |
| x |
点评:本题考查了函数的奇偶性、单调性等基础知识,以及利用函数思想解决不等式恒成立问题的基本思路.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
i为虚数单位,若
=
,则z等于( )
. |
| z |
| 1+7i |
| 1-i |
| A、-3+4i | B、3+4i |
| C、-3-4i | D、3-4i |
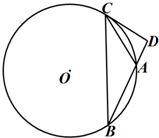
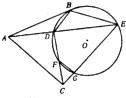 如图,AB是⊙O的切线,B为切点,ADE是⊙O的割线,C是⊙O外一点,且AB=AC,连接BD,BE,CD,CE,CD交⊙O于F,CE交⊙O于G.
如图,AB是⊙O的切线,B为切点,ADE是⊙O的割线,C是⊙O外一点,且AB=AC,连接BD,BE,CD,CE,CD交⊙O于F,CE交⊙O于G.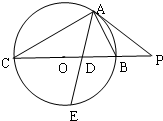 如图,△ABC内接于直径为F1,F2的圆P,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10
如图,△ABC内接于直径为F1,F2的圆P,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10