题目内容
下列命题中的真命题是( )
A、?x∈R,使得sinxcosx=
| ||
| B、?x∈(-∞,0),2x>1 | ||
| C、?x∈R,x2≥x-1 | ||
| D、?x∈(0,π),sinx>cosx |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.利用倍角公式和正弦函数的单调性可得sinxcosx=
sin2x≤
<
,即可判断出;
B.利用指数函数y=2x在R上单调递增,当x∈(-∞,0),可得2x<20=1,即可判断出;
C.?x∈R,利用二次函数的单调性可得:x2-(x-1)=(x-
)2+
≥
>0,即可得出;
D.举反例:x=
,sin
=
<
=cos
即可判断出.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
B.利用指数函数y=2x在R上单调递增,当x∈(-∞,0),可得2x<20=1,即可判断出;
C.?x∈R,利用二次函数的单调性可得:x2-(x-1)=(x-
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
D.举反例:x=
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
解答:
解:A.∵sinxcosx=
sin2x≤
<
,因此不存在x∈R,使得sinxcosx=
成立;
B.∵指数函数y=2x在R上单调递增,若x∈(-∞,0),则2x<20=1,因此不存在x∈(-∞,0),
使得2x>1成立,因此不正确;
C.?x∈R,则x2-(x-1)=(x-
)2+
≥
>0,因此C正确;
D.?x∈(0,π),sinx>cosx,不成立.例如x=
,sin
=
<
=cos
.因此不正确.
综上可知:只有C正确.
故选:C.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
B.∵指数函数y=2x在R上单调递增,若x∈(-∞,0),则2x<20=1,因此不存在x∈(-∞,0),
使得2x>1成立,因此不正确;
C.?x∈R,则x2-(x-1)=(x-
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
D.?x∈(0,π),sinx>cosx,不成立.例如x=
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
综上可知:只有C正确.
故选:C.
点评:本题综合考查了指数函数、二次函数与三角函数的单调性及其倍角公式,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
下列判断错误的是( )
| A、命题“?x∈R,2x>0”的否定是“?x0∈R,2x0≤0” | ||||
| B、命题“若xy=0,则x=0”的否命题为“若xy≠0,则x≠0” | ||||
C、“sinα=
| ||||
| D、函数y=2x-3+1的图象恒过定点A(3,2) |
设集合S={0,a},T={x∈Z|x2<2},则“a=1”是“S⊆T”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
下列说法中,正确的是( )
| A、命题“存在x∈R,x2-x>0”的否定是“对任意x∈R,x2-x<0”. |
| B、设α,β为两个不同的平面,直线l?α,则“l⊥β”是“α⊥β”成立的必要不充分条件. |
| C、命题“若a<b,则am2<bm2”的否命题是真命题. |
| D、已知x∈R,则“x>1”是“x>2”的充分不必要条件. |
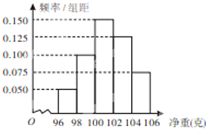 给出下列五个命题:
给出下列五个命题: 下列是容量为100的样本的频率分布直方图,则样本数据落在范围〔6,10〕内的频数值为
下列是容量为100的样本的频率分布直方图,则样本数据落在范围〔6,10〕内的频数值为