题目内容
14.等差数列{an}的前n项和为Sn,已知f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,且f(a2-2)=-$\frac{\sqrt{3}}{2}$,f(a2014-2)=$\frac{\sqrt{3}}{2}$,则S2015=4030.分析 f(x)在R上为奇函数,从而得到a2+a4=4,由此利用等差数列性质能求出S2015.
解答 解:∵f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,
∴$f(-x)=\frac{{2}^{-x}-1}{{2}^{-x}+1}$=$\frac{1-{2}^{x}}{1+{2}^{x}}$=-f(x),
∴f(x)在R上为奇函数,
∵f(a2-2)=-$\frac{\sqrt{3}}{2}$,f(a2014-2)=$\frac{\sqrt{3}}{2}$,
∴a2-2=-(a2014-2),即a2+a2014=4,
∴S2015=$\frac{2015}{2}({a}_{1}+{a}_{2015})$=$\frac{2015}{2}({a}_{2}+{a}_{2014})$=4030.
故答案为:4030.
点评 本题考查等差数列前2015项和的求法,是中档题,解题时要注意函数的奇偶性和等差数列性质的合理运用.

练习册系列答案
相关题目
4.某运输公司接受了向四川地震灾区每天至少运送180t支援物资的任务.该公司有8辆载重6t的A型卡车与4辆载重为10t的B型卡车,有10名驾驶员,每辆卡车每天往返的次数是A型卡车4次,B型卡车3次;每辆卡车往返的成本费是A型卡车320元,B型卡车504元.
(1)设所需A型、B型卡车分别为x辆和y辆,每天A型车和B型车往返的成本费之和为z,请完成如表的空格;
(2)请为公司安排一下,应如何调配车辆,才能使公司所花的往返成本费最低?
(1)设所需A型、B型卡车分别为x辆和y辆,每天A型车和B型车往返的成本费之和为z,请完成如表的空格;
| A型车 | B型车 | 限量 | |
| 车辆数 | x | y | 0≤x≤8,0≤y≤4 |
| 每天运物吨数 | 24x | 30y | 24x+30y≥180 |
| 每天往返成本费 | 320x | 504y | z |
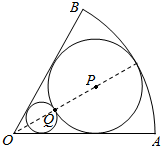 如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.
如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.