题目内容
5.在直角坐标系xoy中,已知点A,B,C是圆x2+y2=4上的动点,且满足AC⊥BC,若点P的坐标为(0,3),则|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$|的最大值为11.分析 由AC⊥BC,AB为直径,可设A(-2,0),B(2,0),C(m,n),且m2+n2=4,求得|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$|,可得几何意义,即为圆上的点与(0,9)的距离,连接PO,延长交圆于D,计算即可得到所求最大值.
解答 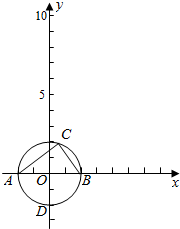 解:由AC⊥BC,AB为直径,可设A(-2,0),B(2,0),
解:由AC⊥BC,AB为直径,可设A(-2,0),B(2,0),
C(m,n),且m2+n2=4,
点P的坐标为(0,3),
即有|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$|=|(-2,-3)+(2,-3)+(m,n-3)|
=|(m,n-9)|=$\sqrt{{m}^{2}+(n-9)^{2}}$表示圆上的点与(0,9)的距离,
连接PO,延长交圆于D,|PD|即为最大值,
且为9+2=11.
故答案为:11.
点评 本题考查向量的模的最大值,注意运用两点的距离,结合图形分析,考查运算能力,属于中档题.

练习册系列答案
相关题目
13.函数f(x)=log2(-x)的值域是( )
| A. | (0,+∞) | B. | (2,+∞) | C. | (-∞,0) | D. | (-∞,+∞) |