题目内容
13.已知圆C:x2+y2+2x-4y+3=0.(1)在x轴、y轴上截距相等的直线l不过原点且与圆C相切,求直线l的方程;
(2)从圆C外一点P向圆引一条切线,切点为M,O为坐标原点,且MP=OP,求点P的轨迹方程.
分析 (1)求出圆的圆心与半径,设出直线方程,利用直线与圆相切求解即可.
(2)设出P的坐标,利用垂直条件列出方程,求解即可.
解答 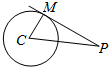 解:(1)C:(x+1)2+(y-2)2=2,显然圆心C(-1,2),半径r=$\sqrt{2}$.
解:(1)C:(x+1)2+(y-2)2=2,显然圆心C(-1,2),半径r=$\sqrt{2}$.
∵不过原点的直线l在x轴、y轴上截距相等
∴不妨设l:$\frac{x}{a}+\frac{y}{a}=1$ 即x+y-a=0
又直线l与圆C相切∴$\frac{|-1+2-a|}{\sqrt{{1}^{2}+{1}^{2}}}$=$\sqrt{2}$,
∴a=3或-1
∴l:x+y-3=0或x+y+1=0
(2)由题如图,PM与圆C相切于M,∴PM⊥CM
设P(x,y),由MP=OP得:OP2=MP2=CP2-r2
∴x2+y2=(x+1)2+(y-2)2-2
整理得:2x-4y+3=0即为所求.
点评 本题考查轨迹方程的求法,圆的方程的求法与应用,考查计算能力.

练习册系列答案
相关题目
1.若直线a∥b,b∩c=A,则a与c的位置关系是( )
| A. | 异面 | B. | 相交 | C. | 平行 | D. | 异面或相交 |
5.若函数f(x)=2sin(ωx-$\frac{π}{3}$)(ω≠0),且f(2+x)=f(2-x),则|ω|的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{5π}{12}$ | D. | $\frac{5π}{6}$ |
2.已知f(x)=ax3+bx+4其中a,b为常数,若f(-2)=-2,则f(2)的值等于( )
| A. | 10 | B. | 6 | C. | -6 | D. | 2 |