题目内容

17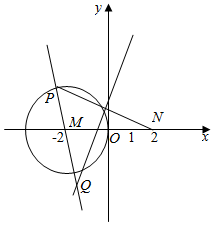．已知P为圆M：（x+2）2+y2=4上的动点，N（2，0），线段PN的垂直平分线与直线PM的交点为Q，点Q的轨迹方程为x2-$\frac{{y}^{2}}{3}$=1．

分析 由中垂线的性质可知|QN|=|PQ|，故而||QN|-|QM||=||PQ|-|QM||=|PM|=2，所以Q的轨迹为以M，N为焦点的双曲线．

解答 解：∵Q在PN的中垂线上，∴|QN|=|PQ|，∴||QN|-|QM||=||PQ|-|QM||=|PM|=2，
∴Q的轨迹为以M，N为焦点的双曲线．
设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$，则$\left\{\begin{array}{l}{c=2}\\{2a=2}\end{array}\right.$，又∵a2+b2=c2，∴a2=1，b2=3，
∴点Q的轨迹方程为x2-$\frac{{y}^{2}}{3}$=1．
故答案为x2-$\frac{{y}^{2}}{3}$=1．

点评 本题考查了双曲线的定义，属于基础题．

练习册系列答案
相关题目
7．在棱长为2的正方体ABCD-A1B1C1D1中，点P是正方体棱上的一点（不包括棱的端点），满足|PB|+|PD1|=$2\sqrt{5}$的点P的个数为12；若满足|PB|+|PD1|=m的点P的个数为6，则m的取值范围是（2$\sqrt{3}$，2$\sqrt{5}$）．
8．已知点F1（-$\sqrt{13}$，0）和点F2（$\sqrt{13}$，0）是椭圆E的两个焦点，且点A（0，6）在椭圆E上．
（1）求椭圆E的方程；
（2）设P是椭圆E上的一点，若|PF2|=4，求以线段PF1为直径的圆的面积．
5．以下四个命题：
①若函数y=ex-mx（x∈R）有大于零的极值点，则实数m＞1；
②若抛物线x2=4y上一点M到焦点的距离为3，则点M到x轴的距离为2；
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；
④已知函数f（x）=x3+ax2+bx-a2-7a在x=1处取得极大值10，则$\frac{a}{b}$的值为-2或-$\frac{2}{3}$．
其中真命题的序号为①②③（写出所有真命题的序号）．
12．运行如图的程序后，输出的结果为（　　）
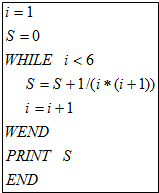
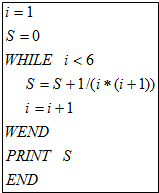
A．$\frac{53}{60}$B．$\frac{4}{5}$C．$\frac{5}{6}$D．$\frac{6}{7}$
2．椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的左，右焦点分别为F1（-1，0），F2（1，0），点P为椭圆上任意一点，且△PF1F2的内切圆面积的最大值为$\frac{1}{3}$π．
（Ⅰ）求椭圆C的方程；
（Ⅱ）直线l：y=kx+b（k＞0，b＞0）是圆O：x2+y2=3的一条切线，且l与椭圆C交于不同的两点A，B．若弦AB的长为$\frac{4\sqrt{6}}{7}$，求直线l的方程．
9．已知二次函数f（x）=x2+2bx+c（b，c∈R）．
（1）若函数y=f（x）的零点为-1和1，求实数b，c的值；
（2）若f（x）满足f（1）=0，且关于x的方程f（x）+x+b=0的两个实数根分别在区间（-3，-2），（0，1）内，求实数b的取值范围．
6．已知集合A={1，2，3}，则B={x-y|x∈A，y∈A}中的元素个数为（　　）
A．9B．5C．3D．1
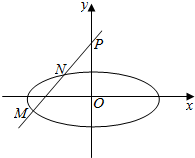7．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（α=2b＞0），直线l过点A（2a，0），B（0，2b），原点O到直线AB的距离为$\frac{4\sqrt{5}}{5}$．
（1）求椭圆的方程；
（2）是否存在过点P（0，2）的直线l与椭圆交于N，M两点，且使$\overrightarrow{QM}$=（λ+1）$\overrightarrow{QN}$-$λ\overrightarrow{QP}$成立（Q为直线l外的一点，λ＞0）？若存在，求λ的取值范围；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网