题目内容
1.方程x2+y2-4x=0表示的圆的圆心和半径分别为( )| A. | (-2,0),2 | B. | (-2,0),4 | C. | (2,0),2 | D. | (2,0),4 |
分析 把圆的方程利用配方法化为标准方程后,即可得到圆心与半径.
解答 解:把圆x2+y2-4x=0的方程化为标准方程得:(x-2)2+y2=4,
所以圆心坐标为(2,0),半径为2,
故选C.
点评 此题比较简单,要求学生会把圆的一般方程化为标准方程.

练习册系列答案
相关题目
11.已知向量$\overrightarrow a=(1,2)$,$\overrightarrow b=(1,0)$,$\overrightarrow c=(3,4)$,若λ为实数,$(\overrightarrow a+λ\overrightarrow b)⊥\overrightarrow c$,则λ=( )
| A. | $\frac{5}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{5}{2}$ | D. | $-\frac{11}{3}$ |
12.已知两条直线y=ax-2和3x-(a+2)y+1=0互相平行,则a等于( )
| A. | -1或3 | B. | -1或3 | C. | 1或3 | D. | 1或-3 |
6.一个三棱锥的三视图如图所示,则三棱锥的体积为( )
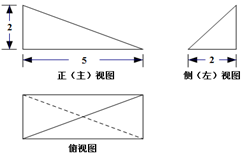

| A. | $\frac{5}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{20}{3}$ | D. | $\frac{25}{3}$ |
13. 如图,在四边形ABCD中,AD=DC=CB=1,$AB=\sqrt{3}$,对角线$AC=\sqrt{2}$.将△ACD沿AC所在直线翻折,当AD⊥BC时,线段BD的长度为$\sqrt{2}$.
如图,在四边形ABCD中,AD=DC=CB=1,$AB=\sqrt{3}$,对角线$AC=\sqrt{2}$.将△ACD沿AC所在直线翻折,当AD⊥BC时,线段BD的长度为$\sqrt{2}$.
 如图,在四边形ABCD中,AD=DC=CB=1,$AB=\sqrt{3}$,对角线$AC=\sqrt{2}$.将△ACD沿AC所在直线翻折,当AD⊥BC时,线段BD的长度为$\sqrt{2}$.
如图,在四边形ABCD中,AD=DC=CB=1,$AB=\sqrt{3}$,对角线$AC=\sqrt{2}$.将△ACD沿AC所在直线翻折,当AD⊥BC时,线段BD的长度为$\sqrt{2}$.
10.△ABC各角的对应边分别为a,b,c,满足$\frac{a}{b+c}+\frac{b}{a+c}≥1$,则角C的范围是( )
| A. | $(0,\frac{π}{3}]$ | B. | $(0,\frac{π}{6}]$ | C. | $[\frac{π}{3},π)$ | D. | $[\frac{π}{6},π)$ |
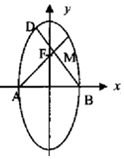 已知椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),F为椭圆是上焦点,点A,B分别为椭圆的左右顶点,过点B作AF的垂线,垂足为N.
已知椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),F为椭圆是上焦点,点A,B分别为椭圆的左右顶点,过点B作AF的垂线,垂足为N.