题目内容

11．已知向量$\overrightarrow a=（1，2）$，$\overrightarrow b=（1，0）$，$\overrightarrow c=（3，4）$，若λ为实数，$（\overrightarrow a+λ\overrightarrow b）⊥\overrightarrow c$，则λ=（　　）
A．$\frac{5}{3}$B．$\frac{1}{2}$C．$-\frac{5}{2}$D．$-\frac{11}{3}$

分析 由平面向量坐标运算法则先求出$\overrightarrow{a}+λ\overrightarrow{b}$，再由$（\overrightarrow a+λ\overrightarrow b）⊥\overrightarrow c$，利用向量垂直的性质，能求出λ．

解答 解：∵$\overrightarrow a=（1，2）$，$\overrightarrow b=（1，0）$，$\overrightarrow c=（3，4）$，λ为实数，
∴$\overrightarrow{a}+λ\overrightarrow{b}$=（1+λ，2），
∵$（\overrightarrow a+λ\overrightarrow b）⊥\overrightarrow c$，
∴（$\overrightarrow{a}+λ\overrightarrow{b}$）•$\overrightarrow{c}$=3（1+λ）+8=0，
解得λ=-$\frac{11}{3}$．
故选：D．

点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意平面向量坐标运算法则和向量垂直的性质的合理运用．

练习册系列答案
相关题目
1．在四棱锥P-ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=$\sqrt{3}$，BC=PA=1，E为PD的中点，点N在面PAC内，且NE⊥平面PAC，则点N到AB的距离为$\frac{\sqrt{10-4\sqrt{3}}}{4}$．
2．下列函数中，既是偶函数，又是在区间（0，+∞）上单调递减的是（　　）
A．$y=\frac{1}{x}$B．y=2|x|C．$y=ln\frac{1}{|x|}$D．y=x3
19．函数f（x）的定义域为D，若x1，x2∈D且当f（x1）=f（x2）时总有x1=x2，则称f（x）为单值函数．例如，函数f（x）=2x+1（x∈R）是单值函数，给出下列命题：
①反比例函数$f（x）=\frac{1}{x}$（x∈R，x≠0）是单值函数；
②二次函数f（x）=x2（x∈R）是单值函数；
③在定义域D上单调递增或递减的函数一定是单值函数．
以上命题中的真命题有①③（写出所有真命题的编号）．
6．已知函数f（x）=e|lnx|，则函数y=f（x+1）的大致图象为（　　）
A．B．C．D． 
16．已知函数$f（x）=1+2sin（{2ωx+\frac{π}{6}}）$（其中0＜ω＜2），若直线$x=\frac{π}{6}$是函数f（x）图象的一条对称轴．
（1）求ω及f（x）的最小正周期；
（2）求函数f（x）$x∈[{-\frac{π}{2}\;，\;\;\frac{π}{2}}]$的单调减区间．
（3）若f（x）与g（x）关于$（{\frac{π}{4}\;，\;\;0}）$对称，求g（x）在区间$[{0\;，\;\;\frac{π}{2}}]$的值域．
3．已知函数f（x）的导函数f'（x），且满足关系式f（x）=x2+4xf'（2）+lnx，则f'（2）的值等于$-\frac{3}{2}$．
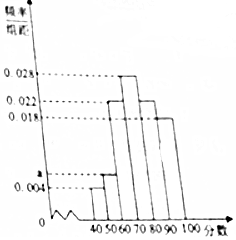20．高三（3）班班主任根据本班50名学生体能测试成绩，绘制频率分布直方图（如图所示），其中样本数据分组区间为[40，50），[50，60），…，[80，90），[90，100]．
（1）求频率分布图中a的值；
（2）求该班50名学生中，成绩不低于80分的概率；
（3）从成绩在[40，60）的学生中，随机抽取2人，求此2人分数都在[40，50）的概率．
1．方程x2+y2-4x=0表示的圆的圆心和半径分别为（　　）
A．（-2，0），2B．（-2，0），4C．（2，0），2D．（2，0），4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网