题目内容
10.△ABC各角的对应边分别为a,b,c,满足$\frac{a}{b+c}+\frac{b}{a+c}≥1$,则角C的范围是( )| A. | $(0,\frac{π}{3}]$ | B. | $(0,\frac{π}{6}]$ | C. | $[\frac{π}{3},π)$ | D. | $[\frac{π}{6},π)$ |
分析 化简已知不等式可得a2+b2-c2≥ab,利用余弦定理得$cosC≥\frac{1}{2}$,利用余弦函数的图象和性质可求C的范围.
解答 解:由$\frac{a}{b+c}+\frac{b}{a+c}≥1$,得:a(a+c)+b(b+c)≥(b+c)(a+c),
化简得:a2+b2-c2≥ab,
同除以2ab,利用余弦定理得,$cosC≥\frac{1}{2}$,
所以$0<C≤\frac{π}{3}$,
故选:A.
点评 本题主要考查了余弦定理,余弦函数的图象和性质在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
1.方程x2+y2-4x=0表示的圆的圆心和半径分别为( )
| A. | (-2,0),2 | B. | (-2,0),4 | C. | (2,0),2 | D. | (2,0),4 |
5.直线y=x-4与曲线y=$\sqrt{2x}$及x轴所围成图形的面积是( )
| A. | $\frac{64}{3}$ | B. | $\frac{40}{3}$ | C. | $\frac{56}{3}$ | D. | $\frac{38}{3}$ |
15.在等差数列{an}中,已知a3+a8>0,且S9<0,则S1、S2、…S9中最小的是( )
| A. | S5 | B. | S6 | C. | S7 | D. | S8 |
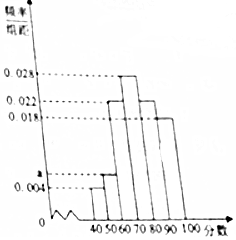 高三(3)班班主任根据本班50名学生体能测试成绩,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].
高三(3)班班主任根据本班50名学生体能测试成绩,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].