题目内容
 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.(1)求证:AB∥平面DEG;
(2)求异面直线BD与CF所成角的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)利用线面平行的判定;(2)向量法.
解答:
(1)证明:∵AD∥EF,EF∥BC,
∴AD∥BC.
又∵BC=2AD,G是BC的中点,
∴AD∥GB,AD=GB,
∴四边形ADGB是平行四边形,
∴AB∥DG.
∵AB?平面DGE,DG?平面DEG,
∴AB∥平面DEG…7分
(2)解:∵EF⊥面AEB,AE?面AEB,BE?面AEB,
∴EF⊥AE,EF⊥BE,又AE⊥EB∴EB,EF,EA两两垂直,
以E为坐标原点,EB,EF,EA分别为
x、y、z轴建立空间直角坐标系,
由已知得,B(2,0,0),D(0,2,2),C(2,4,0),F(0,3,0),…8分
=(2,0,0),
=(-2,-1,0),∴cos<
,
>=
=
,
∴异面直线BD与CF所成角的余弦值
…14分
∴AD∥BC.
又∵BC=2AD,G是BC的中点,
∴AD∥GB,AD=GB,
∴四边形ADGB是平行四边形,
∴AB∥DG.
∵AB?平面DGE,DG?平面DEG,
∴AB∥平面DEG…7分
(2)解:∵EF⊥面AEB,AE?面AEB,BE?面AEB,
∴EF⊥AE,EF⊥BE,又AE⊥EB∴EB,EF,EA两两垂直,
以E为坐标原点,EB,EF,EA分别为
x、y、z轴建立空间直角坐标系,
由已知得,B(2,0,0),D(0,2,2),C(2,4,0),F(0,3,0),…8分
| BD |
| CF |
| BD |
| CF |
| 4-2 | ||||
2
|
| ||
| 15 |
∴异面直线BD与CF所成角的余弦值
| ||
| 15 |
点评:本题考查线面平行的判定,考查异面直线所成角的求法,解题时要认真审题,仔细解答,注意向量法的合理运用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
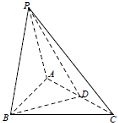 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.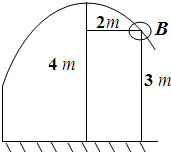 有一次姚明投篮时,测得投篮的轨迹是抛物线,如图所示,抛物线最高点离地面距离4m,篮筐B高为3m,篮筐中心离最高点的水平距离为2m,求投中时抛物线的方程?
有一次姚明投篮时,测得投篮的轨迹是抛物线,如图所示,抛物线最高点离地面距离4m,篮筐B高为3m,篮筐中心离最高点的水平距离为2m,求投中时抛物线的方程?