题目内容
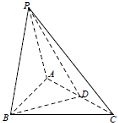 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.(Ⅰ)求证:平面PAB⊥平面ABC
(Ⅱ)如果三棱锥P-BCD的体积为3,求PA.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:计算题,空间位置关系与距离
分析:(Ⅰ)利用面面垂直的判定,证明OD⊥平面PAB,从而平面PAB⊥平面ABC;
(Ⅱ)利用三棱锥的体积公式,得到PA长度的方程,求解即可.
(Ⅱ)利用三棱锥的体积公式,得到PA长度的方程,求解即可.
解答:
 解:(Ⅰ)取AB中点为O,连结OD,OP.
解:(Ⅰ)取AB中点为O,连结OD,OP.
因为PA=PB,所以AB⊥OP.
又AB⊥PD,OP∩PD=P,所以AB⊥平面POD,
因为OD?平面POD,所以AB⊥OD.…(3分)
由已知,BC⊥PB,又OD∥BC,所以OD⊥PB,
因为AB∩PB=B,所以OD⊥平面PAB.
又OD?平面ABC,所以平面PAB⊥平面ABC.…(6分)
(Ⅱ)由(Ⅰ)知,OP⊥平面ABC.
设PA=a,因为D为AC的中点,所以
VP-BCD=
VP-ABC=
×
×
a2×
a=
a3,…(10分)
由
a3=3解得a=2
,即PA=2
.…(12分)
 解:(Ⅰ)取AB中点为O,连结OD,OP.
解:(Ⅰ)取AB中点为O,连结OD,OP.因为PA=PB,所以AB⊥OP.
又AB⊥PD,OP∩PD=P,所以AB⊥平面POD,
因为OD?平面POD,所以AB⊥OD.…(3分)
由已知,BC⊥PB,又OD∥BC,所以OD⊥PB,
因为AB∩PB=B,所以OD⊥平面PAB.
又OD?平面ABC,所以平面PAB⊥平面ABC.…(6分)
(Ⅱ)由(Ⅰ)知,OP⊥平面ABC.
设PA=a,因为D为AC的中点,所以
VP-BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 24 |
由
| ||
| 24 |
| 3 |
| 3 |
点评:本题以考查面面垂直、三棱锥体积计算,考查空间想象能力和计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
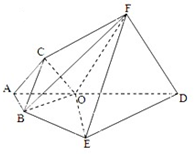 如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODF,△ODE都是正三角形.
如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODF,△ODE都是正三角形. 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.