题目内容
中心在原点、焦点在x轴上的椭圆C的焦距为2,两准线间的距离为10.设点A(5,0),过点A作直线l交椭圆C于P,Q两点,过点P作x轴的垂线交椭圆C于另一点S.
(1) 求椭圆C的方程;
(2) 求证:直线SQ过x轴上一定点B;
(3) 若过点A作直线与椭圆C只有一个公共点D,求过B,D两点、且以AD为切线的圆的方程.
(1) 设椭圆的标准方程为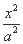 +
+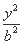 =1(a>b>0),
=1(a>b>0),
依题意得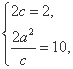 得
得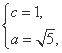 所以b2=4.
所以b2=4.
所以椭圆的标准方程为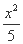 +
+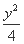 =1.
=1.
(2) 设P(x1,y1),Q(x2,y2),AP=tAQ,
则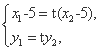
结合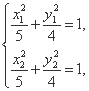 得
得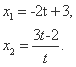
设B(x,0),则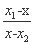 =t,x=
=t,x=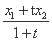 =1,
=1,
所以直线SQ过x轴上一定点B(1,0).
(3) 设过点A的直线方程为y=k(x-5),代入椭圆方程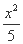 +
+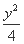 =1得(4+5k2)x2-50k2x+125k2-20=0.
=1得(4+5k2)x2-50k2x+125k2-20=0.
依题意,得Δ=0,即(50k2)2-4(4+5k2)(125k2-20)=0,
解得k=±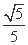 ,且方程的根为x=1.
,且方程的根为x=1.
所以D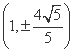 .
.
当点D位于x轴上方时,过点D与AD垂直的直线与x轴交于点E,直线DE的方程是
y-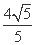 =
=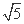 (x-1),所以E
(x-1),所以E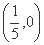 .
.
所求的圆即为以线段DE为直径的圆,方程为
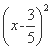 +
+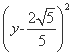 =
=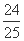 ;
;
同理可得当点D位于x轴下方时,圆的方程为
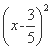 +
+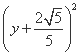 =
=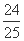 .
.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
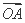 +
+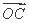 |=
|=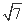 (O为坐标原点),求向量
(O为坐标原点),求向量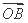 与
与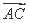 ⊥
⊥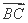 ,求点C的坐标.
,求点C的坐标.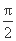 ,AB=AC=AA1=1,延长A1C1 至点P,使C1P=A1C1,连接AP交棱CC1于点D.求:
,AB=AC=AA1=1,延长A1C1 至点P,使C1P=A1C1,连接AP交棱CC1于点D.求: A1D
A1D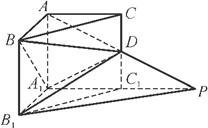
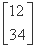 ,N=
,N= .
.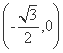 ,F2
,F2
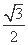 ,0
,0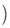 ,点P是第一象限内双曲线上的点,且tan∠PF1F2=
,点P是第一象限内双曲线上的点,且tan∠PF1F2=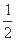 ,tan∠PF2F1=-2,则双曲线的离心率为 .
,tan∠PF2F1=-2,则双曲线的离心率为 . 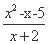 的最小值为 .
的最小值为 .  个单位长度,所得图象的函数解析式为 .
个单位长度,所得图象的函数解析式为 .  ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.