题目内容
已知双曲线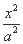 -
-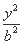 =1(a>0,b>0)的两个焦点为F1
=1(a>0,b>0)的两个焦点为F1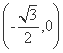 ,F2
,F2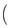
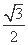 ,0
,0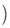 ,点P是第一象限内双曲线上的点,且tan∠PF1F2=
,点P是第一象限内双曲线上的点,且tan∠PF1F2=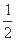 ,tan∠PF2F1=-2,则双曲线的离心率为 .
,tan∠PF2F1=-2,则双曲线的离心率为 .
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
题目内容
已知双曲线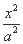 -
-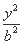 =1(a>0,b>0)的两个焦点为F1
=1(a>0,b>0)的两个焦点为F1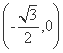 ,F2
,F2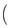
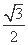 ,0
,0 ,点P是第一象限内双曲线上的点,且tan∠PF1F2=
,点P是第一象限内双曲线上的点,且tan∠PF1F2=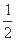 ,tan∠PF2F1=-2,则双曲线的离心率为 .
,tan∠PF2F1=-2,则双曲线的离心率为 .
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案