题目内容
本公司计划在甲、乙两个电视台做总时间不超过300min的广告,广告总费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问:该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大?最大收益是多少万元?
设公司在甲电视台和乙电视台做广告的时间分别为xmin和ymin,总收益为z元.
由题意得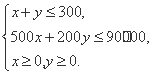 目标函数为z=3 000x+2 000y.
目标函数为z=3 000x+2 000y.
二元一次不等式组等价于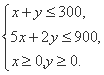
作出二元一次不等式组所表示的可行域.

如图,作直线l:3 000x+2 000y=0,即3x+2y=0,平移直线l,
从图中可知,当直线l过点M时,目标函数取得最大值.
联立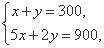 解得x=100,y=200.
解得x=100,y=200.
所以点M的坐标为(100,200).
所以zmax=3 000x+2 000y=700 000(元).
答:该公司在甲电视台做100min广告,在乙电视台做200min广告,公司的收益最大.最大收益是70万元.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
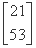 ,B=
,B= ,X=
,X=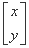 ,试解方程AX=B.
,试解方程AX=B.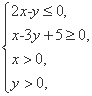 那么z=
那么z=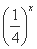 ·
·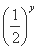 的最小值为 .
的最小值为 . 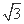 cosωx),设函数f(x)=a·b+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈
cosωx),设函数f(x)=a·b+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈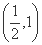 .
.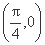 ,求函数f(x)在区间
,求函数f(x)在区间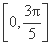 上的取值范围.
上的取值范围.