题目内容
已知点A(2,0),B(0,2),点C(x,y)在以原点为圆心的单位圆上.
(1) 若|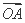 +
+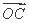 |=
|=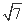 (O为坐标原点),求向量
(O为坐标原点),求向量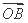 与
与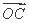 的夹角θ;
的夹角θ;
(2) 若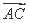 ⊥
⊥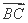 ,求点C的坐标.
,求点C的坐标.
(1) 由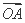 =(2,0),
=(2,0),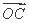 =(x,y),得
=(x,y),得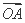 +
+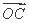 =(2+x,y).
=(2+x,y).
由|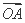 +
+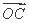 |=
|=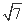 ,得(2+x)2+y2=7,
,得(2+x)2+y2=7,
所以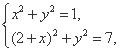 解得x=
解得x=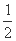 ,y=±
,y=±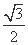 .
.
cos θ=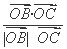 =
= =y=±
=y=±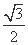 ,
,
所以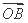 与
与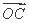 的夹角为30°或150°.
的夹角为30°或150°.
(2) 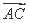 =(x-2,y),
=(x-2,y),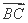 =(x,y-2),由
=(x,y-2),由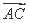 ⊥
⊥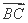 ,得
,得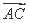 ·
·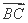 =0,则x2-2x+y2-2y=0.
=0,则x2-2x+y2-2y=0.
由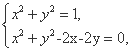
解得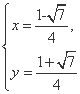 或
或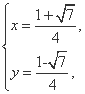
所以点C的坐标为
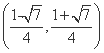 或
或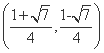 .
.

练习册系列答案
相关题目
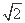 )是极小值,f(
)是极小值,f(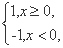 f(x)=x2-2x(x2-a)φ(x2-a).
f(x)=x2-2x(x2-a)φ(x2-a).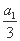 +b1,
+b1,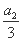 +b2,
+b2,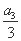 +b3成等比数列,求数列{bn}的前n项和Tn.
+b3成等比数列,求数列{bn}的前n项和Tn.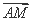 =λ
=λ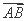 +μ
+μ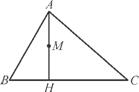
 A1B1C1的底面边长为2 cm,高为5 cm,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为 cm.
A1B1C1的底面边长为2 cm,高为5 cm,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为 cm.