题目内容
已知定义域为R的函数f(x)满足:f(x+2)=
,且x∈[-1,1]时,f(x)=|x|-1,则当x∈[-6,-4]时,f(x)的最小值为( )
| f(x) |
| 2 |
| A、-8 | ||
| B、-4 | ||
C、-
| ||
D、-
|
考点:抽象函数及其应用,函数的定义域及其求法,函数的周期性
专题:计算题,函数的性质及应用
分析:由f(x+2)=
,求出f(x+4)=
,f(x+6)=
,令-5≤x≤-4,则-1≤x+4≤0,求出f(x+4)、f(x)和最小值;令-6≤x≤-5,则0≤x+6≤1,求出f(x+6)、f(x)和最小值,从而确定最小值.
| f(x) |
| 2 |
| f(x) |
| 4 |
| f(x) |
| 8 |
解答:
解:∵f(x+2)=
,
∴f(x+4)=
=
,f(x+6)=
=
,
令-5≤x≤-4,则-1≤x+4≤0,
∵x∈[-1,1]时,f(x)=|x|-1,
∴f(x+4)=|x+4|-1,
∴-5≤x≤-4时,f(x)=4(|x+4|-1),
当x=-4时,f(x)的最小值为-4;
令-6≤x≤-5,则0≤x+6≤1,f(x+6)=|x+6|-1,
∴-6≤x≤-5时,f(x)=8(|x+6|-1),
当x=-6时,f(x)的最小值为-8.
∴当x∈[-6,-4]时,f(x)的最小值为-8.
故选:A.
| f(x) |
| 2 |
∴f(x+4)=
| f(x+2) |
| 2 |
| f(x) |
| 4 |
| f(x+4) |
| 2 |
| f(x) |
| 8 |
令-5≤x≤-4,则-1≤x+4≤0,
∵x∈[-1,1]时,f(x)=|x|-1,
∴f(x+4)=|x+4|-1,
∴-5≤x≤-4时,f(x)=4(|x+4|-1),
当x=-4时,f(x)的最小值为-4;
令-6≤x≤-5,则0≤x+6≤1,f(x+6)=|x+6|-1,
∴-6≤x≤-5时,f(x)=8(|x+6|-1),
当x=-6时,f(x)的最小值为-8.
∴当x∈[-6,-4]时,f(x)的最小值为-8.
故选:A.
点评:本题考查函数的解析式的求法,注意对x的赋值,将未知的范围转化到已知的范围,充分运用条件即可,同时考查绝对值函数的最值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
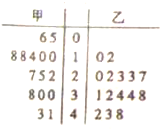 从甲乙两个城市分别随机抽取15台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为
从甲乙两个城市分别随机抽取15台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=5sin6x是( )
A、周期是
| ||
| B、周期是3π的偶函数 | ||
C、周期是
| ||
D、周期是
|
已知双曲线
-
=1(a>0,b>0)的右焦点与抛物线y2=12x的焦点重合,且双曲线的一条渐近线被圆(x-3)2+y2=8截得的弦长为4,则此双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±2
|
一个样本容量为20的样本数据,它们组成一个等差数列{an},若a1=4,a20=42,则此样本的平均数和中位数分别是( )
| A、22,23 |
| B、23,22 |
| C、23,24 |
| D、23,23 |
已知数列{an}是等差数列,a1+a3+a5=105,a2+a4+a6=99,{an}的前n项和为Sn,则使得Sn达到最大的n是( )
| A、18 | B、19 | C、20 | D、21 |