题目内容
5.设a是函数$f(x)={2^x}-{log_{\frac{1}{2}}}$x的零点,若x0>a,则f(x0)的值满足( )| A. | f(x0)=0 | B. | f(x0)<0 | C. | f(x0)>0 | D. | f(x0)的符号不确定 |
分析 作出y=2x和y=log${\;}_{\frac{1}{2}}$x的函数图象,根据函数图象判断2${\;}^{{x}_{0}}$和log${\;}_{\frac{1}{2}}$x0的大小关系.
解答 解:作出y=2x和y=log${\;}_{\frac{1}{2}}$x的函数图象,如图:
由图象可知当x0>a时,2${\;}^{{x}_{0}}$>log${\;}_{\frac{1}{2}}$x0,
∴f(x0)=2${\;}^{{x}_{0}}$-log${\;}_{\frac{1}{2}}$x0>0.
故选:C.
点评 本题考查了函数的零点的定义,函数的单调性,利用函数图象可方便快速判断出答案.

练习册系列答案
相关题目
10.设数列{an}和{bn}分别是等差数列与等比数列,且a1=b1=9,a7=b7=1,则以下结论正确的是( )
| A. | a3<a4 | B. | a4>b4 | C. | a4<b4 | D. | b3<b4 |
11.若tan($\frac{π}{4}$-α)=-$\frac{1}{3}$,则sin(2α+$\frac{π}{4}$)的值为( )
| A. | $\frac{7\sqrt{2}}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | $\frac{7}{10}$ |
8.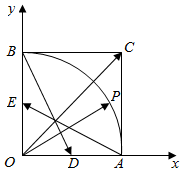 如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
 如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )| A. | -$\sqrt{2}$ | B. | -2 | C. | -$\sqrt{3}$ | D. | -2$\sqrt{2}$ |
10.若命题p:0是偶数,命题q:2是3的约数,则下列命题中为真的是( )
| A. | p且q | B. | p或q | C. | 非p | D. | 以上都不对 |
17.已知向量$\vec a$,$\vec b$的夹角为60°,且$|{\vec a}|=2$,$|{\vec b}|=1$,当$|{\vec a-x\vec b}|$取得最小值时,实数x的值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
15.为得到函数y=cos(2x+$\frac{π}{3}$)的图象,只需将函数y=sin2x的图象( )
| A. | 向左平移$\frac{5π}{12}$个单位长度 | B. | 向右平移$\frac{5π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{5π}{6}$个单位长度 | D. | 向右平移$\frac{5π}{6}$个单位长度 |