题目内容
14.下列几个命题:①若函数$f(x)={e^{-{{(x-m)}^2}}}$为偶函数,则m=0;
②若f(x)的定义域为[0,1],则f(x+2)的定义域为[-2,-1];
③函数y=log2(-x+1)+2的图象可由y=log2(-x-1)-2的图象向上平移4个单位向左平移2个单位得到;
④若关于x方程|x2-2x-3|=m有两解,则m=0或m>4;
其中正确的有①、②、④.
分析 ①判断函数的对称性,利用偶函数的定义和性质进行判断.
②根据复合函数定义域之间的关系进行判断.
③根据函数图象之间的关系进行判断.
④利用数形结合以及一元二次函数的性质进行判断.
解答 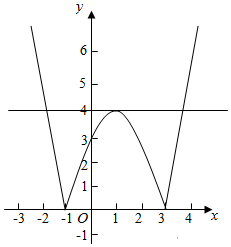 解:①若∵函数$f(x)={e^{-{{(x-m)}^2}}}$关于x=m对称,∴若f(x)为偶函数,则m=0;故①正确,
解:①若∵函数$f(x)={e^{-{{(x-m)}^2}}}$关于x=m对称,∴若f(x)为偶函数,则m=0;故①正确,
②若f(x)的定义域为[0,1],由0≤x+2≤1得-2≤x≤-1,即则f(x+2)的定义域为[-2,-1];故②正确,
③由y=log2(-x-1)-2的图象向上平移4个单位得到由y=log2(-x-1)-2+4=log2(-x-1)+2,然后向左平移2个单位,得到y═log2[-(x+2)-1]+2=log2(-x-3)+2,故③错误,
④设f(x)=|x2-2x-3|,作出函数f(-x)的图象如图,若f(x)=m有两解,则m=0或m>4;故④正确,
故答案为:①、②、④.
点评 本题主要考查命题的真假判断,涉及函数的定义域,图象,奇偶性的性质,综合考查函数的性质的应用,但难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.过点M(-1,3)且与直线l:x-y=0仅有一个交点的直线有( )
| A. | 0条 | B. | 1条 | C. | 2条 | D. | 无数条 |
5.设a是函数$f(x)={2^x}-{log_{\frac{1}{2}}}$x的零点,若x0>a,则f(x0)的值满足( )
| A. | f(x0)=0 | B. | f(x0)<0 | C. | f(x0)>0 | D. | f(x0)的符号不确定 |
6.将函数y=$2{cos^2}(x-\frac{π}{4})$的图象沿x轴向右平移a(a>0)个单位后,所得图象关于y轴对称,则a的最小值为( )
| A. | $\frac{3}{4}π$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
4.已知集合A={-1,0,1,2},B={1,x,x2-x},且B⊆A,则x=( )
| A. | 1 | B. | 0 | C. | 2 | D. | -1 |