题目内容
8.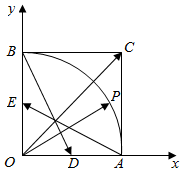 如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )| A. | -$\sqrt{2}$ | B. | -2 | C. | -$\sqrt{3}$ | D. | -2$\sqrt{2}$ |
分析 由条件即可得到${\overrightarrow{AE}}^{2}={\overrightarrow{BD}}^{2}=\frac{5}{4}$,${\overrightarrow{OP}}^{2}=1$,且可求出$\overrightarrow{AE}•\overrightarrow{BD}=-1$,从而对$\overrightarrow{OP}=x\overrightarrow{AE}+y\overrightarrow{BD}$两边平方便可得到$1=\frac{5}{4}({x}^{2}+{y}^{2})-2xy$,根据x2+y2≥2xy便可得到xy≤2,而由题意可知x,y<0,$\overrightarrow{OC}=(1,1)$,从而得出$\overrightarrow{a}•\overrightarrow{OC}=x+y≤-2\sqrt{xy}$,而$-2\sqrt{xy}≥-2\sqrt{2}$,这样即可求出x+y的最大值,即$\overrightarrow{a}•\overrightarrow{OC}$的最大值.
解答 解:根据条件得,${\overrightarrow{AE}}^{2}=\frac{5}{4},{\overrightarrow{BD}}^{2}=\frac{5}{4}$,${\overrightarrow{OP}}^{2}=1$,$\overrightarrow{AE}•\overrightarrow{BD}=(\frac{1}{2}\overrightarrow{OB}-\overrightarrow{OA})•(\frac{1}{2}\overrightarrow{OA}-\overrightarrow{OB})$=$0-\frac{1}{2}-\frac{1}{2}+0=-1$;
∴${\overrightarrow{OP}}^{2}=(x\overrightarrow{AE}+y\overrightarrow{BD})^{2}$
=${x}^{2}{\overrightarrow{AE}}^{2}+2xy\overrightarrow{AE}•\overrightarrow{BD}+{y}^{2}{\overrightarrow{BD}}^{2}$
=$\frac{5}{4}({x}^{2}+{y}^{2})-2xy$
=1;
∴${x}^{2}+{y}^{2}=\frac{4}{5}(2xy+1)≥2xy$;
∴xy≤2;
据题意知,x<0,y<0,$\overrightarrow{OC}=(1,1)$;
∴$\overrightarrow{a}•\overrightarrow{OC}=x+y=-[(-x)+(-y)]≤-2\sqrt{xy}$;
由xy≤2得,$\sqrt{xy}≤\sqrt{2},-2\sqrt{xy}≥-2\sqrt{2}$;
∴$x+y≤-2\sqrt{2}$,当且仅当$x=y=-\sqrt{2}$时取“=”;
∴$\overrightarrow{a}•\overrightarrow{OC}$的最大值为$-2\sqrt{2}$.
故选:D.
点评 考查直角三角形边的关系,向量减法和数乘的几何意义,向量垂直的充要条件,以及向量数量积的运算,不等式x2+y2≥2xy和基本不等式的运用,向量数量积的坐标运算,相等向量和向量坐标的概念.

| A. | 0条 | B. | 1条 | C. | 2条 | D. | 无数条 |
| A. | d>$\frac{12}{19}$ | B. | d<$\frac{2}{3}$ | C. | $\frac{12}{19}$≤d<$\frac{2}{3}$ | D. | $\frac{12}{19}$<d≤$\frac{2}{3}$ |
| A. | f(x0)=0 | B. | f(x0)<0 | C. | f(x0)>0 | D. | f(x0)的符号不确定 |